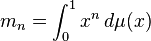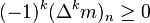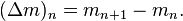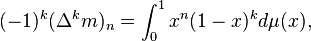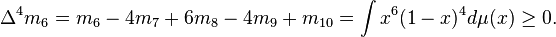Hausdorff moment problem

In mathematics, the Hausdorff moment problem, named after Felix Hausdorff, asks for necessary and sufficient conditions that a given sequence { mn : n = 0, 1, 2, ... } be the sequence of moments

m_n = \int_0^1 x^n\,d\mu(x)\,

of some Borel measure μ supported on the closed unit interval [0, 1]. In the case m0 = 1, this is equivalent to the existence of a random variable X supported on [0, 1], such that E Xn = mn.

The essential difference between this and other well-known moment problems is that this is on a bounded interval, whereas in the Stieltjes moment problem one considers a half-line [0, ∞), and in the Hamburger moment problem one considers the whole line (−∞, ∞).

In 1921, Hausdorff showed that { mn : n = 0, 1, 2, ... } is such a moment sequence if and only if the sequence is completely monotonic, i.e., its difference sequences satisfy the equation

(-1)^k(\Delta^k m)_n \geq 0

for all n,k ≥ 0. Here, Δ is the difference operator given by

(\Delta m)_n = m_{n+1} - m_n.

The necessity of this condition is easily seen by the identity

(-1)^k(\Delta^k m)_n = \int_0^1 x^n (1-x)^k d\mu(x),

which is ≥ 0, being the integral of an almost sure non-negative function. For example, it is necessary to have

\Delta^4 m_6 = m_6 - 4m_7 + 6m_8 - 4m_9 + m_{10} = \int x^6 (1-x)^4 d\mu(x) \geq 0.

See also

References

External links