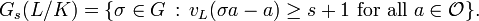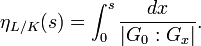Hasse–Arf theorem
In mathematics, specifically in local class field theory, the Hasse–Arf theorem is a result concerning jumps of the upper numbering filtration of the Galois group of a finite Galois extension. A special case of it was originally proved by Helmut Hasse,[1][2] and the general result was proved by Cahit Arf.[3][4]
Statement
Higher ramification groups
The theorem deals with the upper numbered higher ramification groups of a finite abelian extension L/K. So assume L/K is a finite Galois extension, and that vK is a discrete normalised valuation of K, whose residue field has characteristic p > 0, and which admits a unique extension to L, say w. Denote by vL the associated normalised valuation ew of L and let  be the valuation ring of L under vL. Let L/K have Galois group G and define the s-th ramification group of L/K for any real s ≥ −1 by
be the valuation ring of L under vL. Let L/K have Galois group G and define the s-th ramification group of L/K for any real s ≥ −1 by
So, for example, G−1 is the Galois group G. To pass to the upper numbering one has to define the function ψL/K which in turn is the inverse of the function ηL/K defined by
The upper numbering of the ramification groups is then defined by Gt(L/K) = Gs(L/K) where s = ψL/K(t).
These higher ramification groups Gt(L/K) are defined for any real t ≥ −1, but since vL is a discrete valuation, the groups will change in discrete jumps and not continuously. Thus we say that t is a jump of the filtration {Gt(L/K) : t ≥ −1} if Gt(L/K) ≠ Gu(L/K) for any u > t. The Hasse–Arf theorem tells us the arithmetic nature of these jumps
Statement of the theorem
With the above set up, the theorem states that the jumps of the filtration {Gt(L/K) : t ≥ −1} are all rational integers.[4][5]
Example
Suppose G is cyclic of order 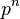 ,
,  residue characteristic and
residue characteristic and 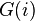 be the subgroup of
be the subgroup of  of order
of order 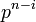 . The theorem says that there exist positive integers
. The theorem says that there exist positive integers 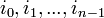 such that
such that
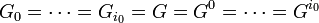
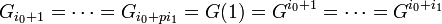
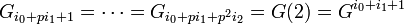
- ...
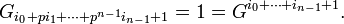 [4]
[4]
Notes
- ↑ H. Hasse, Führer, Diskriminante und Verzweigunsgskörper relativ Abelscher Zahlkörper, J. Reine Angew. Math. 162 (1930), pp.169–184.
- ↑ H. Hasse, Normenresttheorie galoisscher Zahlkörper mit Anwendungen auf Führer und Diskriminante abelscher Zahlkörper, J. Fac. Sci. Tokyo 2 (1934), pp.477–498.
- ↑ Arf, C. (1939). "Untersuchungen über reinverzweigte Erweiterungen diskret bewerteter perfekter Körper". J. Reine Angew. Math. (in German) 181: 1–44. Zbl 0021.20201.
- ↑ 4.0 4.1 4.2 Serre (1979) IV.3, p.76
- ↑ Neukirch (1999) Theorem 8.9, p.68
References
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, Zbl 0956.11021, MR 1697859
- Serre, Jean-Pierre (1979), Local fields, Graduate Texts in Mathematics 67, Translated from the French by Marvin Jay Greenberg, Springer-Verlag, ISBN 0-387-90424-7, MR 554237, Zbl 0423.12016