Hartogs number
In mathematics, specifically in axiomatic set theory, a Hartogs number is a particular kind of cardinal number. It was shown by Friedrich Hartogs in 1915, from ZF alone (that is, without using the axiom of choice), that there is a least well-ordered cardinal greater than a given well-ordered cardinal.
To define the Hartogs number of a set it is not in fact necessary that the set be well-orderable: If X is any set, then the Hartogs number of X is the least ordinal α such that there is no injection from α into X. If X cannot be well-ordered, then we can no longer say that this α is the least well-ordered cardinal greater than the cardinality of X, but it remains the least well-ordered cardinal not less than or equal to the cardinality of X. The map taking X to α is sometimes called Hartogs' function.
Proof
Given some basic theorems of set theory, the proof is simple. Let 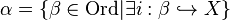 . First, we verify that α is a set.
. First, we verify that α is a set.
- X × X is a set, as can be seen in axiom of power set.
- The power set of X × X is a set, by the axiom of power set.
- The class W of all reflexive well-orderings of subsets of X is a definable subclass of the preceding set, so it is a set by the axiom schema of separation.
- The class of all order types of well-orderings in W is a set by the axiom schema of replacement, as
- (Domain(w), w)
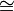 (β, ≤)
(β, ≤)
- (Domain(w), w)
- can be described by a simple formula.
But this last set is exactly α.
Now because a transitive set of ordinals is again an ordinal, α is an ordinal. Furthermore, if there were an injection from α into X, then we would get the contradiction that α ∈ α. It is claimed that α is the least such ordinal with no injection into X. Given β < α, β ∈ α so there is an injection from β into X.
References
- Hartogs, Fritz (1915). "Über das Problem der Wohlordnung". Mathematische Annalen (in German) 76 (4): 438–443. doi:10.1007/BF01458215. JFM 45.0125.01. Available at the DigiZeitschriften.
- Jech, Thomas (2002). Set theory, third millennium edition (revised and expanded). Springer. ISBN 3-540-44085-2.
- Charles Morgan. "Axiomatic set theory". Course Notes. University of Bristol. Retrieved 2010-04-10.