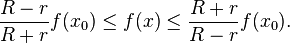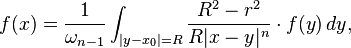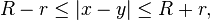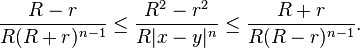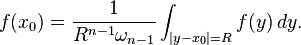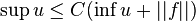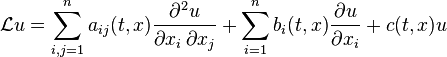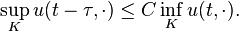Harnack's inequality

In mathematics, Harnack's inequality is an inequality relating the values of a positive harmonic function at two points, introduced by A. Harnack (1887). J. Serrin (1955) and J. Moser (1961, 1964) generalized Harnack's inequality to solutions of elliptic or parabolic partial differential equations. Perelman's solution of the Poincaré conjecture uses a version of the Harnack inequality, found by R. Hamilton (1993), for the Ricci flow. Harnack's inequality is used to prove Harnack's theorem about the convergence of sequences of harmonic functions. Harnack's inequality can also be used to show the interior regularity of weak solutions of partial differential equations.

The statement

A harmonic function (green) over a disk (blue) is bounded from above by a function (red) that coincides with the harmonic function at the disk center and approaches infinity towards the disk boundary.

Harnack's inequality applies to a non-negative function f defined on a closed ball in Rⁿ with radius R and centre x₀. It states that, if f is continuous on the closed ball and harmonic on its interior, then for any point x with |x - x₀| = r < R

\displaystyle{{1-(r/R)\over [1+(r/R)]^{n-1}}f(x_0)\le f(x) \le {1+(r/R)\over [1-(r/R)]^{n-1}} f(x_0).}

In the plane R² (n = 2) the inequality can be written:

{R-r\over R+r} f(x_0)\le f(x)\le {R+r\over R-r}f(x_0).

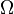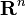For general domains $\Omega$ in $\mathbf{R}^n$ the inequality can be stated as follows: If 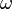$\omega$ is a bounded domain with 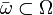$\bar{\omega} \subset \Omega$ , then there is a constant $C$ such that

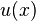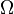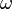for every twice differentiable, harmonic and nonnegative function $u(x)$ . The constant $C$ is independent of $u$ ; it depends only on the domains $\Omega$ and $\omega$ .

Proof of Harnack's inequality in a ball

By Poisson's formula

\displaystyle{f(x) = {1\over \omega_{n-1}} \int_{|y-x_0|=R} {R^2 -r^2\over R|x-y|^n}\cdot f(y)\, dy,}

where ω_{n − 1} is the area of the unit sphere in Rⁿ and r = |x - x₀|.

Since

\displaystyle{R-r \le |x-y| \le R+r,}

the kernel in the integrand satisfies

\displaystyle{{R -r\over R (R+r)^{n-1}} \le {R^2 -r^2\over R|x-y|^n}\le {R+r\over R(R-r)^{n-1}}.}

Harnack's inequality follows by substituting this inequality in the above integral and using the fact that the average of a harmonic function over a sphere equals it value at the center of the sphere:

\displaystyle{f(x_0)={1\over R^{n-1}\omega_{n-1}} \int_{|y-x_0|=R} f(y)\, dy.}

Elliptic partial differential equations

For elliptic partial differential equations, Harnack's inequality states that the supremum of a positive solution in some connected open region is bounded by some constant times the infimum, possibly with an added term containing a functional norm of the data:

\sup u \le C ( \inf u + ||f||)

The constant depends on the ellipticity of the equation and the connected open region.

Parabolic partial differential equations

There is a version of Harnack's inequality for linear parabolic PDEs such as heat equation.

Let 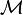$\mathcal{M}$ be a smooth domain in 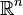$\mathbb{R}^n$ and consider the linear parabolic operator

\mathcal{L}u=\sum_{i,j=1}^n a_{ij}(t,x)\frac{\partial^2 u}{\partial x_i\,\partial x_j}+\sum_{i=1}^n b_i(t,x)\frac{\partial u}{\partial x_i} + c(t,x)u

with smooth and bounded coefficients and a nondegenerate matrix 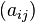$(a_{ij})$ . Suppose that 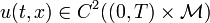$u(t,x)\in C^2((0,T)\times\mathcal{M})$ is a solution of

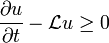\frac{\partial u}{\partial t}-\mathcal{L}u\ge0

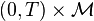
(0,T)\times\mathcal{M}

such that

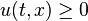\quad u(t,x)\ge0

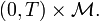
\quad(0,T)\times\mathcal{M}.

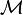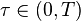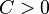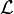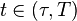Let $K$ be a compact subset of $\mathcal{M}$ and choose $\tau\in(0,T)$ . Then there exists a constant $\quad C>0$ (depending only on $K$ , $\tau$ and the coefficients of $\mathcal{L}$ ) such that, for each $\quad t\in(\tau,T)$ ,

\sup_K u(t-\tau,\cdot)\le C\inf_K u(t,\cdot).\,

References