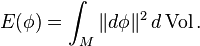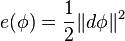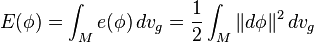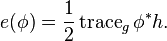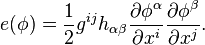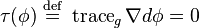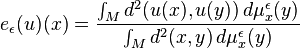Harmonic map

This article is about harmonic maps between Riemannian manifolds. For harmonic functions, see harmonic function.

A (smooth) map φ:M→N between Riemannian manifolds M and N is called harmonic if it is a critical point of the Dirichlet energy functional

E(\phi) = \int_M \|d\phi\|^2\, d\operatorname{Vol}.

This functional E will be defined precisely below—one way of understanding it is to imagine that M is made of rubber and N made of marble (their shapes given by their respective metrics), and that the map φ:M→N prescribes how one "applies" the rubber onto the marble: E(φ) then represents the total amount of elastic potential energy resulting from tension in the rubber. In these terms, φ is a harmonic map if the rubber, when "released" but still constrained to stay everywhere in contact with the marble, already finds itself in a position of equilibrium and therefore does not "snap" into a different shape.

Harmonic maps are the 'least expanding' maps in orthogonal directions.

Existence of harmonic maps from a complete Riemannian manifold to a complete Riemannian manifold of non-positive sectional curvature was proved by Eells & Sampson (1964).

Mathematical definition

Given Riemannian manifolds (M,g), (N,h) and φ as above, the energy density of φ at a point x in M is defined as

e(\phi) = \frac12\|d\phi\|^2

where the 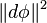\|d\phi\|^2 is the squared norm of the differential of \phi, with respect to the induced metric on the bundle 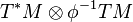T^*M \otimes \phi^{-1} T M. The total energy of φ is given by integrating the density over M

E(\phi) = \int_M e(\phi)\, dv_g = \frac{1}{2} \int_M \|d\phi\|^2\, dv_g

where dvg denotes the measure on M induced by its metric. This generalizes the classical Dirichlet energy.

The energy density can be written more explicitly as

e(\phi) = \frac12\operatorname{trace}_g\phi^*h.

Using the Einstein summation convention, in local coordinates the right hand side of this equality reads

e(\phi) = \frac12g^{ij}h_{\alpha\beta}\frac{\partial\phi^\alpha}{\partial x^i}\frac{\partial\phi^\beta}{\partial x^j}.

If M is compact, then φ is called a harmonic map if it is a critical point of the energy functional E. This definition is extended to the case where M is not compact by requiring the restriction of φ to every compact domain to be harmonic, or, more typically, requiring that φ be a critical point of the energy functional in the Sobolev space H1,2(M,N).

Equivalently, the map φ is harmonic if it satisfies the Euler-Lagrange equations associated to the functional E. These equations read

\tau(\phi)\ \stackrel{\text{def}}{=}\ \operatorname{trace}_g\nabla d\phi = 0

where ∇ is the connection on the vector bundle T*M⊗φ−1(TN) induced by the Levi-Civita connections on M and N. The quantity τ(φ) is a section of the bundle φ−1(TN) known as the tension field of φ. In terms of the physical analogy, it corresponds to the direction in which the "rubber" manifold M will tend to move in N in seeking the energy-minimizing configuration.

Examples

Problems and applications

Harmonic maps between metric spaces

The energy integral can be formulated in a weaker setting for functions u : M → N between two metric spaces (Jost 1995). The energy integrand is instead a function of the form

e_\epsilon(u)(x) = \frac{\int_M d^2(u(x),u(y))\,d\mu^\epsilon_x(y)}{\int_M d^2(x,y)\,d\mu^\epsilon_x(y)}

in which με
x is a family of measures attached to each point of M.

References

External links