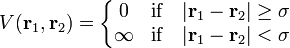Hard spheres
Hard spheres are widely used as model particles in the statistical mechanical theory of fluids and solids. They are defined simply as impenetrable spheres that cannot overlap in space. They mimic the extremely strong repulsion that atoms and spherical molecules experience at very close distances. Hard spheres systems are studied by analytical means, by molecular dynamics simulations, and by the experimental study of certain colloidal model systems.
Formal definition
Hard spheres of diameter  are particles with the following pairwise interaction potential:
are particles with the following pairwise interaction potential:
where 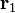 and
and 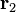 are the positions of the two particles.
are the positions of the two particles.
Hard-spheres gas
The first three virial coefficients for hard spheres can be determined analytically
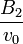
= 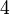
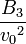
= 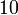
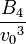
= 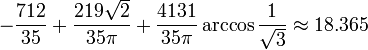
Higher-order ones can be determined numerically using Monte Carlo integration. We list
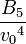
= 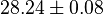
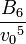
= 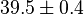
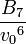
= 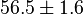
A table of virial coefficients for up to eight dimensions can be found on the page Hard sphere: virial coefficients.

 as a function of the volume fraction (or packing fraction)
as a function of the volume fraction (or packing fraction) 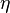
The hard sphere system exhibits a fluid-solid phase transition between the volume fractions of freezing 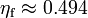 and melting
and melting 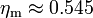 . The pressure diverges at random close packing
. The pressure diverges at random close packing 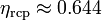 for the metastable liquid branch and at close packing
for the metastable liquid branch and at close packing 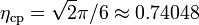 for the stable solid branch.
for the stable solid branch.
Hard-spheres liquid
The static structure factor of the hard-spheres liquid can be calculated using the Percus–Yevick approximation.
Literature
- J. P. Hansen and I. R. McDonald Theory of Simple Liquids Academic Press, London (1986)
- Hard sphere model page on SklogWiki.