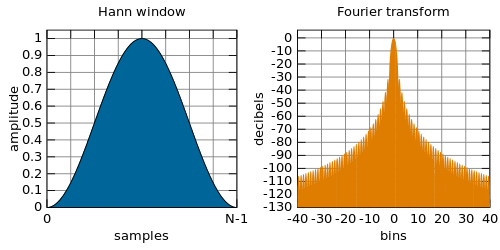
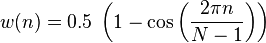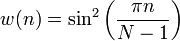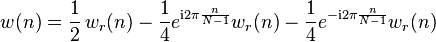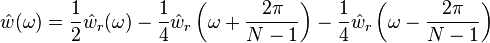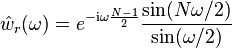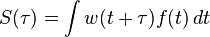Hann function

Hann function with B = 1.50 (left), and its frequency response (right)

The Hann function, named after the Austrian meteorologist Julius von Hann, is a discrete window function given by

w(n)= 0.5\; \left(1 - \cos \left ( \frac{2 \pi n}{N-1} \right) \right)

w(n)= \sin^2 \left ( \frac{ \pi n}{N-1} \right)

or, in terms of the haversine function,

w(n)=\operatorname{haversin}\left(\frac {2 \pi n} {N-1} \right).

Spectrum

The Hann window is a linear combination of modulated rectangular windows $w_r = \mathbf{1}_{[0,N-1]}$ . Thanks to the Euler formula

w(n)= \frac{1}{2} \,w_r(n) -\frac{1}{4} e^{\mathrm{i}2\pi \frac{n}{N-1}} w_r(n) - \frac{1}{4}e^{-\mathrm{i}2\pi \frac{n}{N-1}} w_r(n)

Thanks to the basic properties of the Fourier transform, its spectrum is

\hat{w} (\omega) = \frac{1}{2} \hat{w}_r (\omega) - \frac{1}{4} \hat{w}_r \left(\omega + \frac{2\pi}{N-1}\right) - \frac{1}{4} \hat{w}_r \left(\omega - \frac{2\pi}{N-1}\right)

with the spectrum of the rectangular window

\hat{w}_r (\omega) = e^{-\mathrm{i} \omega \frac{N-1}{2}} \frac{\sin(N\omega/2)}{\sin(\omega/2)}

(the modulation factor vanished if windows are time-shifted around 0)

Name

Hann function is the original name, in honour of von Hann; however, the erroneous "Hanning" function is also heard of on occasion, derived from the paper in which it was named, where the term "hanning a signal" was used to mean applying the Hann window to it. The confusion arose from the similar Hamming function, named after Richard Hamming.

Use

The Hann function is typically used as a window function in digital signal processing to select a subset of a series of samples in order to perform a Fourier transform or other calculations.

i.e. (using continuous version to illustrate)

S(\tau)= \int w(t+\tau)f(t) \, dt

Such windows are also widely called "Hanning windows" and "Hann'd".

The advantage of the Hann window is very low aliasing, and the tradeoff is slightly decreased resolution (widening of the main lobe). If the Hann window is used to sample a signal in order to convert to frequency domain, it is complex to reconvert to the time domain without adding distortions.

References

Harris, F. J. (1978). "On the use of windows for harmonic analysis with the discrete Fourier transform". Proceedings of the IEEE 66: 51. doi:10.1109/PROC.1978.10837.
Blackman, R. B.; Tukey, J. W. (1958). "The Measurement of Power Spectra from the Point of View of Communications Engineering - Part I". Bell System Technical Journal 37: 185. doi:10.1002/j.1538-7305.1958.tb03874.x.

External links

Hann function at MathWorld

Hann function

Spectrum

Name

Use

See also

References

External links