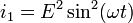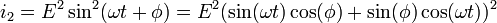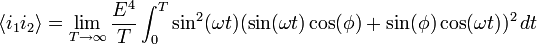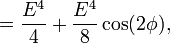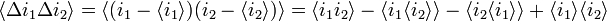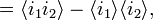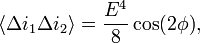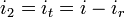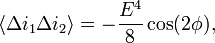Hanbury Brown and Twiss effect

In physics, the Hanbury Brown and Twiss (HBT) effect is any of a variety of correlation and anti-correlation effects in the intensities received by two detectors from a beam of particles. HBT effects can generally be attributed to the dual wave-particle nature of the beam, and the results of a given experiment depend on whether the beam is composed of fermions or bosons. Devices which use the effect are commonly called intensity interferometers and were originally used in astronomy, although they are also heavily used in the field of quantum optics.

History

In 1956, Robert Hanbury Brown and Richard Q. Twiss published A test of a new type of stellar interferometer on Sirius, in which two photomultiplier tubes (PMTs), separated by about 6 meters, were aimed at the star Sirius. Light was collected into the PMTs using mirrors from searchlights. An interference effect was observed between the two intensities, revealing a positive correlation between the two signals, despite the fact that no phase information was collected. Hanbury Brown and Twiss used the interference signal to determine the apparent angular size of Sirius, claiming excellent resolution.

Also, in the field of particle physics, Goldhaber et al. performed an experiment in 1959 in Berkeley and found an unexpected angular correlation among identical pions, discovering the ρ0 resonance, by means of 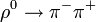\rho^0\rightarrow \pi^-\pi^+ decay.[1] From then on, the HBT technique started to be used by the heavy-ion community to determine the space-time dimensions of the particle emission source for heavy ion collisions. For recent developments in this field, cf. for example the review article by Lisa.[2]

The original HBT result met with much skepticism in the physics community. Although intensity interferometry had been widely used in radio astronomy where Maxwell's equations are valid, at optical wavelengths the light would be quantised into a relatively small number of photons. Many physicists worried that the correlation was inconsistent with the laws of thermodynamics. Some even claimed that the effect violated the uncertainty principle. Hanbury Brown and Twiss resolved the dispute in a neat series of papers (see References below) which demonstrated, first, that wave transmission in quantum optics had exactly the same mathematical form as Maxwell's equations albeit with an additional noise term due to quantisation at the detector, and secondly, that according to Maxwell's equations, intensity interferometry should work. Others, such as Edward Mills Purcell immediately supported the technique, pointing out that the clumping of bosons was simply a manifestation of an effect already known in statistical mechanics. After a number of experiments, the whole physics community agreed that the observed effect was real.

The original experiment used the fact that two bosons tend to arrive at two separate detectors at the same time. Morgan and Mandel used a thermal photon source to create a dim beam of photons and observed the tendency of the photons to arrive at the same time on a single detector. Both of these effects used the wave nature of light to create a correlation in arrival time - if a single photon beam is split into two beams, then the particle nature of light requires that each photon is only observed at a single detector, and so an anti-correlation was observed in 1986. Finally, bosons have a tendency to clump together, giving rise to Bose–Einstein correlations, while fermions due to the Pauli exclusion principle, tend to spread apart leading to Fermi–Dirac (anti)correlations. Bose–Einstein correlations have been observed between pions, kaons and photons, and Fermi–Dirac (anti)correlations between protons, neutrons and electrons. For a general introduction in this field cf. the textbook on Bose–Einstein correlations by Richard M. Weiner [3] A difference in repulsion of BECs in the "trap-and-free fall" analogy of the HBT effect[4] affects comparison.

Wave mechanics

The HBT effect can, in fact, be predicted solely by treating the incident electromagnetic radiation as a classical wave. Suppose we have a single incident wave with frequency \omega on two detectors. Since the detectors are separated, say the second detector gets the signal delayed by a phase of \phi. Since the intensity at a single detector is just the square of the wave amplitude, we have for the intensities at the two detectors

i_1=E^2\sin^2(\omega t)\,
i_2=E^2\sin^2(\omega t + \phi)=E^2(\sin(\omega t)\cos(\phi)+\sin(\phi)\cos(\omega t))^2\,

which makes the correlation

\langle i_1i_2\rangle = \lim_{T\rightarrow\infty}\frac{E^4}{T}\int^T_0 \sin^2(\omega t)(\sin(\omega t)\cos(\phi)+\sin(\phi)\cos(\omega t))^2\,dt
= \frac{E^4}{4}+\frac{E^4}{8}\cos(2\phi),

a constant plus a phase dependent component. Most modern schemes actually measure the correlation in intensity fluctuations at the two detectors, but it is not too difficult to see that if the intensities are correlated then the fluctuations 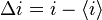\Delta i = i-\langle i\rangle, where 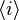\langle i\rangle is the average intensity, ought to be correlated. In general

\langle\Delta i_1\Delta i_2\rangle = \langle(i_1-\langle i_1\rangle)(i_2-\langle i_2\rangle)\rangle =\langle i_1i_2\rangle-\langle i_1\langle i_2\rangle\rangle -\langle i_2\langle i_1\rangle\rangle +\langle i_1\rangle \langle i_2\rangle
=\langle i_1i_2\rangle -\langle i_1\rangle \langle i_2\rangle,

and since the average intensity at both detectors in this example is 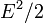E^2/2,

\langle \Delta i_1\Delta i_2\rangle=\frac{E^4}{8}\cos(2\phi),

so our constant vanishes. The average intensity is 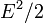E^2/2 because the time average of 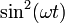\sin^2(\omega t) is 1/2.

An evaluation of the degree of the second-order coherence for complementary[5] (anti-correlated) outputs of an interferometer leads to behaviour like "anti-bunching effect". For example, a variation in reflectivity (and thus also in transmittance) of a beam splitter, where

i_1=i_r\
i_2=i_t=i -i_r\,

results in the negative correlation of fluctuations

\langle \Delta i_1\Delta i_2\rangle=-\frac{E^4}{8}\cos(2\phi),

i.e. a dip in the coherence function 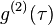g^{(2)}(\tau).

Quantum interpretation

Photon detections as a function of time for a) antibunching (e.g. light emitted from a single atom), b) random (e.g. a coherent state, laser beam), and c) bunching (chaotic light). τc is the coherence time (the time scale of photon or intensity fluctuations).

The above discussion makes it clear that the Hanbury Brown and Twiss (or photon bunching) effect can be entirely described by classical optics. The quantum description of the effect is less intuitive: if one supposes that a thermal or chaotic light source such as a star randomly emits photons, then it is not obvious how the photons "know" that they should arrive at a detector in a correlated (bunched) way. A simple argument suggested by Ugo Fano [Fano, 1961] captures the essence of the quantum explanation. Consider two points a and b in a source which emit photons detected by two detectors A and B as in the diagram. A joint detection takes place when the photon emitted by a is detected by A and the photon emitted by b is detected by B (red arrows) or when a's photon is detected by B and b's by A (green arrows). 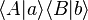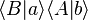The quantum mechanical probability amplitudes for these two possibilities are denoted by \langle A|a \rangle \langle B|b \rangle and \langle B|a \rangle \langle A|b \rangle respectively. If the photons are indistinguishable, the two amplitudes interfere constructively to give a joint detection probability greater than that for two independent events. 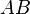The sum over all possible pairs a,b in the source washes out the interference unless the distance AB is sufficiently small.

Fano's explanation nicely illustrates the necessity of considering two particle amplitudes, which are not as intuitive as the more familiar single particle amplitudes used to interpret most interference effects. This may help to explain why some physicists in the 1950s had difficulty accepting the Hanbury Brown Twiss result. But the quantum approach is more than just a fancy way to reproduce the classical result: if the photons are replaced by identical fermions such as electrons, the antisymmetry of wave functions under exchange of particles renders the interference destructive, leading to zero joint detection probability for small detector separations. This effect is referred to as antibunching of fermions [Henny, 1999]. The above treatment also explains photon antibunching [Kimble, 1977]: if the source consists of a single atom which can only emit one photon at a time, simultaneous detection in two closely spaced detectors is clearly impossible. Antibunching, whether of bosons or of fermions, has no classical wave analog.

From the point of view of the field of quantum optics, the HBT effect was important to lead physicists (among them Roy J. Glauber and Leonard Mandel) to apply quantum electrodynamics to new situations, many of which had never been experimentally studied, and in which classical and quantum predictions differ.

See also

References

  1. ↑ Phys.Rev.Lett.3,p181(1959)
  2. ↑ M.Lisa,et al., Ann.Rev.Nucl.Part.Sci 55, p357(2005), ArXiv 0505014
  3. ↑ Richard M. Weiner, Introduction to Bose–Einstein Correlations and Subatomic Interferometry, John Wiley, 2000
  4. ↑ Comparison of the Hanbury Brown-Twiss effect for bosons and fermions - http://arxiv.org/abs/cond-mat/0612278
  5. ↑ Modern Interferometry - http://www.teachspin.com/instruments/moderni/experiments.shtml

Note that Hanbury Brown is not hyphenated.

- the cavity-QED equivalent for Kimble & Mandel's free-space demonstration of photon antibunching in resonance fluorescence

External links