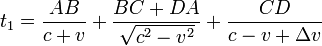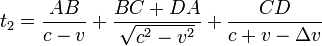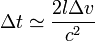Hammar experiment

The Hammar experiment was an experiment designed and conducted by Gustaf Wilhelm Hammar (1935) to test the aether drag hypothesis. Its negative result refuted some specific aether drag models, and confirmed special relativity.

Overview

Experiments such as the Michelson–Morley experiment of 1887 (and later other experiments such as the Trouton–Noble experiment in 1903 or the Trouton-Rankine experiment in 1908), presented evidence against the theory of a medium for light propagation known as the Luminiferous aether; a theory that had been an established part of science for nearly one hundred years at the time. These results cast doubts on what was then a very central assumption of modern science, and later led to the development of special relativity. In an attempt to explain the results of the Michelson–Morley experiment in the context of the assumed medium, aether, many new hypotheses were examined. One of the proposals was that instead of passing through a static and unmoving aether, massive objects at the Earth's surface may drag some of the aether along with them, making it impossible to detect a "wind". Oliver Lodge (1893-1897) was one of the first to perform a test of this theory by using rotating and massive lead blocks in an experiment that attempted to cause an asymmetrical aether wind. His tests yielded no appreciable results differing from previous tests for the aether wind.[1][2]

In the 1920s, Dayton Miller conducted repetitions of the Michelson–Morley experiments, which allegedly gave a positive result. However, several experiments conducted afterwards by others gave negative results. Miller claimed that this is due to entrainment of the aether, because the other experiments used heavily enclosed equipment. To test Miller's assertion, Hammar conducted the following experiment using a common path interferometer in 1935.[3][4]

The experiment

Using a half-silvered mirror A, he divided a ray of white light into two half-rays. One half-ray was sent in the transverse direction into a heavy walled steel pipe terminated with lead plugs. In this pipe, the ray was reflected by mirror D and sent into the longitudinal direction to another mirror C at the other end of the pipe. There it was reflected and sent in the transverse direction to a mirror B outside of the pipe. From B it traveled back to A in the longitudinal direction. The other half-ray traversed the same path in the opposite direction.

The topology of the light path was that of a Sagnac interferometer with an odd number of reflections. Sagnac interfometers offer excellent contrast and fringe stability,[5] and the configuration with an odd number of reflections is only slightly less stable than the configuration with an even number of reflections. (With an odd number of reflections, the oppositely traveling beams are laterally inverted with respect to each other over most of the light path, so that the topology deviates slightly from strict common path.[6]) The relative immunity of his apparatus to vibration, mechanical stress and temperature effects, allowed Hammar to detect fringe displacements as little as 1/10 of a fringe, despite using the interferometer outdoors in an open environment with no temperature control.

Similar to Lodge's experiment, Hammar's apparatus should have caused an asymmetry in any proposed aether wind. Hammar's expectation of the results was that: With the apparatus aligned perpendicular to the aether wind, both long arms would be equally affected by aether entrainment. With the apparatus aligned parallel to the aether wind, one arm would be more affected by aether entrainment than the other. The following expected propagation times for the counter-propagating rays were given by Robertson/Noonan:[4]

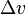t_{1}=\frac{AB}{c+v}+\frac{BC+DA}{\sqrt{c^{2}-v^{2}}}+\frac{CD}{c-v+\Delta v}
t_{2}=\frac{AB}{c-v}+\frac{BC+DA}{\sqrt{c^{2}-v^{2}}}+\frac{CD}{c+v-\Delta v}

where \Delta v is the velocity of the entrained aether. This gives an expected time difference:

\Delta t\simeq\frac{2l\Delta v}{c^{2}}

On September 1, 1934, Hammar set up the apparatus on top of a high hill two miles south of Moscow, Idaho, and made many observations with the apparatus turned in all directions of the azimuth during the daylight hours of September 1, 2, and 3. He saw no shift of the interference fringes, corresponding to an upper limit of 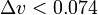\Delta v<0.074 km/s.[3] These results are considered a proof against the aether drag hypothesis as it was proposed by Miller.[4]

Consequences for Aether drag hypothesis

Because differing ideas of "aether drag" existed, the interpretation of all aether drag experiments can be done in the context of each version of the hypothesis.

  1. None or partial entrainment by any object with mass. This was discussed by scientists such as Augustin-Jean Fresnel and François Arago. It was refuted by the Michelson–Morley experiment.
  2. Complete entrainment within or in the vicinity of all masses. It was refuted by the Aberration of light, Sagnac effect, Oliver Lodge's experiments, and Hammar's experiment.
  3. Complete entrainment within or in the vicinity of only very large masses such as Earth. It was refuted by the Aberration of light, Michelson–Gale–Pearson experiment.

References

  1. ↑ Lodge, Oliver J. (1893). "Aberration Problems". Philosophical Transactions of the Royal Society A 184: 727–804. Bibcode:1893RSPTA.184..727L. doi:10.1098/rsta.1893.0015.
  2. ↑ Lodge, Oliver J. (1897). "Experiments on the Absence of Mechanical Connexion between Ether and Matter". Philosophical Transactions of the Royal Society A 189: 149–166. Bibcode:1897RSPTA.189..149L. doi:10.1098/rsta.1897.0006.
  3. ↑ 3.0 3.1 G. W. Hammar (1935). "The Velocity of Light Within a Massive Enclosure". Physical Review 48 (5): 462–463. Bibcode:1935PhRv...48..462H. doi:10.1103/PhysRev.48.462.2.
  4. ↑ 4.0 4.1 4.2 H. P. Robertson and Thomas W. Noonan (1968). "Hammar's experiment". Relativity and Cosmology. Philadelphia: Saunders. pp. 36–38.
  5. ↑ "The Sagnac Interferometer". University of Arizona College of Optical Sciences. Retrieved 30 March 2012.
  6. ↑ Hariharan, P (2007). Basics of Interferometry, 2nd edition. Elsevier. p. 19. ISBN 0-12-373589-0.