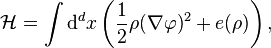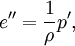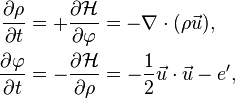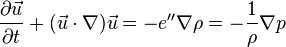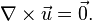Hamiltonian fluid mechanics
Hamiltonian fluid mechanics is the application of Hamiltonian methods to fluid mechanics. This formalism can only apply to nondissipative fluids.
Irrotational barotropic flow
Take the simple example of a barotropic, inviscid vorticity-free fluid.
Then, the conjugate fields are the mass density field ρ and the velocity potential φ. The Poisson bracket is given by
and the Hamiltonian by:
where e is the internal energy density, as a function of ρ. For this barotropic flow, the internal energy is related to the pressure p by:
where an apostrophe ('), denotes differentiation with respect to ρ.
This Hamiltonian structure gives rise to the following two equations of motion:
where 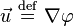 is the velocity and is vorticity-free. The second equation leads to the Euler equations:
is the velocity and is vorticity-free. The second equation leads to the Euler equations:
after exploiting the fact that the vorticity is zero:
See also
References
- Morrison, P.J. (2006). Elsevier, ed. "Hamiltonian Fluid Mechanics". Encyclopedia of Mathematical Physics 2. pp. 593–600.
- Morrison, P. J. (April 1998). "Hamiltonian Description of the Ideal Fluid". Reviews of Modern Physics 70 (2) (Austin, Texas). pp. 467–521. doi:10.1103/RevModPhys.70.467.
- R. Salmon (1988). "Hamiltonian Fluid Mechanics". Annual Review of Fluid Mechanics 20: 225–256. Bibcode:1988AnRFM..20..225S. doi:10.1146/annurev.fl.20.010188.001301.
- T. G. Shepherd (1990). "Symmetries, conservation laws, and Hamiltonian structure in geophysical fluid dynamics". Advances in Geophysics 32: 287–338. Bibcode:1990AdGeo..32..287S. doi:10.1016/S0065-2687(08)60429-X.
- Swaters, Gordon E. (2000). Introduction to Hamiltonian Fluid Dynamics and Stability Theory. Boca Raton, Florida: Chapman & Hall/CRC. p. 274. ISBN 1-58488-023-6.
![[\varphi(\vec{x}),\rho(\vec{y}) ]=\delta^d(\vec{x}-\vec{y})](../I/m/86b67b7fe003a939f97fbf3582b2d935.png)