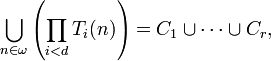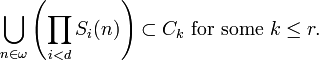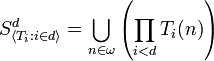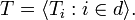Halpern–Läuchli theorem

In mathematics, the Halpern–Läuchli theorem is a partition result about finite products of infinite trees. Its original purpose was to give a model for set theory in which the Boolean prime ideal theorem is true but the axiom of choice is false. It is often called the Halpern–Läuchli theorem, but the proper attribution for the theorem as it is formulated below is to Halpern–Läuchli–Laver–Pincus or HLLP (named after James D. Halpern, Hans Läuchli, Richard Laver, and David Pincus), following (Milliken 1979).

Let d,r < ω, 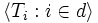$\langle T_i: i \in d \rangle$ be a sequence of finitely splitting trees of height ω. Let

\bigcup_{n \in \omega} \left(\prod_{i<d}T_i(n)\right) = C_1 \cup \cdots \cup C_r,

then there exists a sequence of subtrees 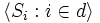$\langle S_i: i \in d \rangle$ strongly embedded in 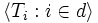$\langle T_i: i \in d \rangle$ such that

\bigcup_{n \in \omega} \left(\prod_{i<d}S_i(n)\right) \subset C_k\text{ for some }k \le r.

Alternatively, let

S^d_{\langle T_i: i \in d \rangle} = \bigcup_{n \in \omega} \left(\prod_{i<d}T_i(n)\right)

and

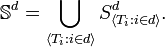\mathbb{S}^d=\bigcup_{\langle T_i: i \in d \rangle} S^d_{\langle T_i: i \in d \rangle}.

The HLLP theorem says that not only is the collection 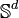$\mathbb{S}^d$ partition regular for each d < ω, but that the homogeneous subtree guaranteed by the theorem is strongly embedded in

T= \langle T_i: i \in d \rangle.\

References

J.D. Halpern and H. Läuchli, A partition theorem, Trans. Amer. Math. Soc. 124 (1966), 360–367
Keith R. Milliken, A Ramsey Theorem for Trees, J. Comb. Theory (Series A) 26 (1979), 215–237
Keith R. Milliken, A Partition Theorem for the Infinite Subtrees of a Tree, Trans. Amer. Math. Soc. 263 No.1 (1981), 137–148
J.D. Halpern and David Pincus, Partitions of Products, Trans. Amer. Math. Soc. 267, No.2 (1981), 549–568.