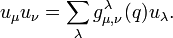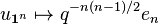Hall algebra
In mathematics, the Hall algebra is an associative algebra with a basis corresponding to isomorphism classes of finite abelian p-groups. It was first discussed by E. Steinitz (1901) but forgotten until it was rediscovered by Philip Hall (1959), both of whom published no more than brief summaries of their work. The Hall polynomials are the structure constants of the Hall algebra. The Hall algebra plays an important role in the theory of Kashiwara–Lusztig's canonical bases in quantum groups. Ringel (1990) generalized Hall algebras to more general categories, such as the category of representations of a quiver.
Construction
A finite abelian p-group M is a direct sum of cyclic p-power components 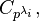 where
where
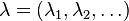 is a partition of
is a partition of  called the type of M. Let
called the type of M. Let 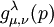 be the number of subgroups N of M such that N has type
be the number of subgroups N of M such that N has type 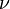 and the quotient M/N has type
and the quotient M/N has type  . Hall proved that the functions g are polynomial functions of p with integer coefficients. Thus we may replace p with an indeterminate q, which results in the Hall polynomials
. Hall proved that the functions g are polynomial functions of p with integer coefficients. Thus we may replace p with an indeterminate q, which results in the Hall polynomials
Hall next constructs an associative ring  over
over ![\mathbb{Z}[q]](../I/m/0ebc1e7bb79974d9c905d206cff48b76.png) , now called the Hall algebra. This ring has a basis consisting of the symbols
, now called the Hall algebra. This ring has a basis consisting of the symbols 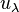 and the structure constants of the multiplication in this basis are given by the Hall polynomials:
and the structure constants of the multiplication in this basis are given by the Hall polynomials:
It turns out that H is a commutative ring, freely generated by the elements 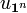 corresponding to the elementary p-groups. The linear map from H to the algebra of symmetric functions defined on the generators by the formula
corresponding to the elementary p-groups. The linear map from H to the algebra of symmetric functions defined on the generators by the formula
(where en is the nth elementary symmetric function) uniquely extends to a ring homomorphism and the images of the basis elements 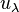 may be interpreted via the Hall–Littlewood symmetric functions. Specializing q to 1, these symmetric functions become Schur functions, which are thus closely connected with the theory of Hall polynomials.
may be interpreted via the Hall–Littlewood symmetric functions. Specializing q to 1, these symmetric functions become Schur functions, which are thus closely connected with the theory of Hall polynomials.
References
- Hall, Philip (1959), "The algebra of partitions", Proceedings of the 4th Canadian mathematical congress, Banff, pp. 147–159
- George Lusztig, Quivers, perverse sheaves, and quantized enveloping algebras. J. Amer. Math. Soc. 4 (1991), no. 2, 365–421.
- Macdonald, I. G. (1995), Symmetric functions and Hall polynomials, Oxford Mathematical Monographs (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR 1354144
- Ringel, Claus Michael (1990), "Hall algebras and quantum groups", Inventiones Mathematicae 101 (3): 583–591, doi:10.1007/BF01231516, MR 1062796
- Schiffmann, O (2006), Lectures on Hall algebras, arXiv:math/0611617
- Steinitz, E. (1901), "Zur Theorie der Abel'schen Gruppen", Jahresbericht der Deutschen Mathematiker-Vereinigung 9: 80–85
![g^\lambda_{\mu,\nu}(q)\in\mathbb{Z}[q]. \,](../I/m/d77f8a8cef2d36f5c6a6a59106911761.png)