Haagerup property

In mathematics, the Haagerup property, named after Uffe Haagerup and also known as Gromov's a-T-menability, is a property of groups that is a strong negation of Kazhdan's property (T). Property (T) is considered a representation-theoretic form of rigidity, so the Haagerup property may be considered a form of strong nonrigidity; see below for details.

The Haagerup property is interesting to many fields of mathematics, including harmonic analysis, representation theory, operator K-theory, and geometric group theory.

Perhaps its most impressive consequence is that groups with the Haagerup Property satisfy the Baum-Connes conjecture and the related Novikov conjecture. Groups with the Haagerup property are also uniformly embeddable into a Hilbert space.

Definitions

Let $G$ be a second countable locally compact group. The following properties are all equivalent, and any of them may be taken to be definitions of the Haagerup property:

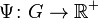There is a proper continuous conditionally negative definite function $\Psi\colon G \to \Bbb{R}^+$ .
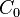$G$ has the Haagerup approximation property, also known as Property $C_0$ : there is a sequence of normalized continuous positive-definite functions 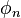$\phi_n$ which vanish at infinity on $G$ and converge to 1 uniformly on compact subsets of $G$ .
There is a strongly continuous unitary representation of $G$ which weakly contains the trivial representation and whose matrix coefficients vanish at infinity on $G$ .
There is a proper continuous affine isometric action of $G$ on a Hilbert space.

Examples

There are many examples of groups with the Haagerup property, most of which are geometric in origin. The list includes:

All compact groups (trivially). Note all compact groups also have property (T). The converse holds as well: if a group has both property (T) and the Haagerup property, then it is compact.
SO(n,1)
SU(n,1)
Groups acting properly on trees or on 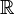$\Bbb{R}$ -trees
Coxeter groups
Amenable groups
Groups acting properly on CAT(0) cubical complexes

References

Cherix, Pierre-Alain; Cowling, Michael; Jolissaint, Paul; Julg, Pierre; Valette, Alain (2001), Groups with the Haagerup property. Gromov's a-T-menability., Progress in Mathematics 197, Basel: Birkhäuser Verlag, doi:10.1007/978-3-0348-8237-8, ISBN 3-7643-6598-6, MR 1852148