Grunsky matrix
In mathematics, the Grunsky matrices, or Grunsky operators, are matrices introduced by Grunsky (1939) in complex analysis and geometric function theory. They correspond to either a single holomorphic function on the unit disk or a pair of holomorphic functions on the unit disk and its complement. The Grunsky inequalities express boundedness properties of these matrices, which in general are contraction operators or in important special cases unitary operators. As Grunsky showed, these inequalities hold if and only if the holomorphic function is univalent. The inequalities are equivalent to the inequalities of Goluzin, discovered in 1947. Roughly speaking, the Grunsky inequalities give information on the coefficients of the logarithm of a univalent function; later generalizations by Milin, starting from the Lebedev–Milin inequality, succeeded in exponentiating the inequalities to obtain inequalities for the coefficients of the univalent function itself. Historically the inequalities were used in proving special cases of the Bieberbach conjecture up to the sixth coefficient; the exponentiated inequalities of Milin were used by de Branges in the final solution. The Grunsky operators and their Fredholm determinants are related to spectral properties of bounded domains in the complex plane. The operators have further applications in conformal mapping, Teichmüller theory and conformal field theory.
If f(z) is a holomorphic univalent function on the unit disk, normalized so that f(0) = 0 and f'(0) = 1, the function
is a non-vanishing univalent function on |z| > 1 having a simple pole at ∞ with residue 1:
The same inversion formula applied to g gives back f and establishes a one-one correspondence between these two classes of function.
The Grunsky matrix (cnm) of g is defined by the equation
It is a symmetric matrix. Its entries are called the Grunsky coefficients of g.
Note that
so that that the coefficients can be expressed directly in terms of f. Indeed if
then for m, n > 0
and d0n = dn0 is given by
with
Grunsky inequalities
If f is a holomorphic function on the unit disk with Grunsky matrix (cnm), the Grunsky inequalities state that
for any finite sequence of complex numbers λ1, ..., λN.
Faber polynomials
The Grunsky coefficients of a normalized univalent function in |z| > 1
are polynomials in the coefficients bi which can be computed recursively in terms of the Faber polynomials Φn, a monic polynomial of degree n depending on g.
Taking the derivative in z of the defining relation of the Grunsky coefficients and multiplying by z gives
The Faber polynomials are defined by the relation
Dividing this relation by z and integrating between z and ∞ gives
This gives the recurrence relations for n > 0
with
Thus
so that for n ≥ 1
The latter property uniquely determines the Faber polynomial of g.
Milin's area theorem
Let g(z) be a univalent function on |z| > 1 normalized so that
and let f(z) be a non-constant holomorphic function on C.
If
is the Laurent expansion on z > 1, then
Proof
If Ω is a bounded open region with smooth boundary ∂Ω and h is a differentiable function on Ω extending to a continuous function on the closure, then, by Stokes theorem applied to the differential 1-form ω = h(z)dz,
For r > 1, let Ωr be the complement of the image of |z|> r under g(z), a bounded domain. Then, by the above identity with h = f', the area of f(Ωr) is given by
Hence
Since the area is non-negative
The result follows by letting r decrease to 1.
Milin's proof of Grunsky inequalities
If
then
Applying Milin's area theorem,
(Equality holds here if and only if the complement of the image of g has Lebesgue measure zero.)
So a fortiori
Hence the symmetric matrix
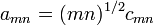 ,
,
regarded as an operator on CN with its standard inner product, satisfies
So by the Cauchy-Schwarz inequality
With 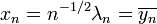 , this gives the Grunsky inequality:
, this gives the Grunsky inequality:
Criterion for univalence
Let g(z) be a holomorphic function on z > 1 with
Then g is univalent if and only if the Grunsky coefficients of g satisfy the Grunsky inequalities for all N.
In fact the conditions have already been shown to be necessary. To see sufficiency, note that
makes sense when |z| and |ζ| are large and hence the coefficients cmn are defined. If the Grunsky inequalities are satisfied then it is easy to see that the |cmn| are uniformly bounded and hence the expansion on the left hand side converges for |z|>1 and |ζ|>1. Exponentiating both sides, this implies that g is univalent.
Pairs of univalent functions
Let F(z) and g(ζ) be univalent holomorphic functions on |z| < 1 and |ζ| > 1, such that their images are disjoint in C. Suppose that these functions are normalized so that
and
with a ≠ 0 and
The Grunsky matrix (cmn) of this pair of functions is defined for all non-zero m and n by the formulas:
with cm, –n = c–n,m for m, n ≥ 1, so that cmn is a symmetric matrix.
In 1972 the American mathematician James Hummel extended the Grunsky inequalities to this matrix, proving that for any sequence of complex numbers λ±1, ..., λ±N
The proof proceeds by computing the area of the image of the complement of the images of |z| < r < 1 under F and |ζ| > R >1 under g under a suitable Laurent polynomial h(w).
Let Φn and Φ-n denote the Faber polynomials of g and 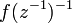 and set
and set
Then for |z| < 1
and for |ζ| > 1
The area equals
where C1 is the image of the circle |ζ| = R under g and C2 is the image of the circle |z| = r under F.
Hence
Since the area is positive, the right hand side must also be positive. Letting r increase to 1 and R decrease to 1, it follows that
with equality if and only if the complement of the images has Lebesgue measure zero.
As in the case of a single function g, this implies the required inequality.
Unitarity
The matrix
of a single function g or a pair of functions F, g is unitary if and only if the complement of the image of g or the union of the images of F and g has Lebesgue measure zero. So, roughly speaking, in the case of one function the image is a slit region in the complex plane; and in the case of two functions the two regions are separated by a closed Jordan curve.
In fact the infinite matrix A acting on the Hilbert space of square summable sequences satisfies
But if J denotes complex conjugation of a sequence, then
since A is symmetric. Hence
so that A is unitary.
Equivalent forms of Grunsky inequalities
Goluzin inequalities
If g(z) is a normalized univalent function in |z| > 1, z1, ..., zN are distinct points with |zn| > 1 and α1, ..., αN are complex numbers, the Goluzin inequalities, proved in 1947 by the Russian mathematician Gennadi Mikhailovich Goluzin (1906-1953), state that
To deduce them from the Grunsky inequalities, let
for k > 0.
Conversely the Grunsky inequalities follow from the Goluzin inequalities by taking
where
with r > 1, tending to ∞.
Bergman–Schiffer inequalities
Bergman & Schiffer (1951) gave another derivation of the Grunsky inequalities using reproducing kernels and singular integral operators in geometric function theory; a more recent related approach can be found in Baranov & Hedenhalm (2008). Let f(z) be a normalized univalent function in |z| < 1, let z1, ..., zN be distinct points with |zn| < 1 and let α1, ..., αN be complex numbers.
The Bergman-Schiffer inequalities state that
To deduce these inequalities from the Grunsky inequalities, set
for k > 0.
Conversely the Grunsky inequalities follow from the Bergman-Schiffer inequalities by taking
where
with r < 1, tending to 0.
Applications
The Grunsky inequalities imply many inequalities for univalent functions. They were also used by Schiffer and Charzynski in 1960 to give a completely elementary proof of the Bieberbach conjecture for the fourth coefficient; a far more complicated proof had previously been found by Schiffer and Garabedian in 1955. In 1968 Pedersen and Ozawa independently used the Grunsky inequalities to prove the conjecture for the sixth coefficient.[1][2]
In the proof of Schiffer and Charzynski, if
is a normalized univalent function in |z| < 1, then
is an odd univalent function in |z| > 1.
Combining Gronwall's area theorem for f with the Grunsky inequalities for the first 2 x 2 minor of the Grunsky matrix of g leads to a bound for |a4| in terms of a simple function of a2 and a free complex parameter. The free parameter can be chosen so that the bound becomes a function of half the modulus of a2 and it can then be checked directly that this function is no greater than 4 on the range [0,1].
As Milin showed, the Grunsky inequalities can be exponentiated. The simplest case proceeds by writing
with an(w) holomorphic in |w| < 1.
The Grunsky inequalities, with λn = wn imply that
On the other hand if
as formal power series, then the first of the Lebedev-Milin inequalities (1965) states that[3][4]
Equivalently the inequality states that if g(z) is a polynomial with g(0) = 0, then
where A is the area of g(D),
To prove the inequality, note that the coefficients are determined by the recursive formula
so that by the Cauchy-Schwarz inequality
The quantities cn obtained by imposing equality here:
satisfy 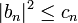 and hence, reversing the steps,
and hence, reversing the steps,
In particular defining bn(w) by the identity
the following inequality must hold for |w| < 1
Beurling transform
The Beurling transform (also called the Beurling-Ahlfors transform and the Hilbert transform in the complex plane) provides one of the most direct methods of proving the Grunsky inequalities, following Bergman & Schiffer (1951) and Baranov & Hedenhalm (2008).
The Beurling transform is defined on L2(C) as the operation of multiplication by 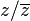 on Fourier transforms. It thus defines a unitary operator. It can also be defined directly as a principal value integral[5]
on Fourier transforms. It thus defines a unitary operator. It can also be defined directly as a principal value integral[5]
For any bounded open region Ω in C it defines a bounded operator TΩ from the conjugate of the Bergman space of Ω onto the Bergman space of Ω: a square integrable holomorphic function is extended to 0 off Ω to produce a function in L2(C) to which T is applied and the result restricted to Ω, where it is holomorphic. If f is a holomorphic univalent map from the unit disk D onto Ω then the Bergman space of Ω and its conjugate can be identified with that of D and TΩ becomes the singular integral operator with kernel
It defines a contraction. On the other hand it can be checked that TD = 0 by computing directly on powers 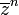 using Stokes theorem to transfer the integral to the boundary.
using Stokes theorem to transfer the integral to the boundary.
It follows that the operator with kernel
acts as a contraction on the conjugate of the Bergman space of D. Hence, if
then
Grunsky operator and Fredholm eigenvalues
If Ω is a bounded domain in C with smooth boundary, the operator TΩ can be regarded as a bounded antilinear contractive operator on the Bergman space H = A2(Ω). It is given by the formula
for u in the Hilbert space H= A2(Ω). TΩ is called the Grunsky operator of Ω (or f). Its realization on D using a univalent function f mapping D onto Ω and the fact that TD = 0 shows that it is given by restriction of the kernel
and is therefore a Hilbert–Schmidt operator.
The antilinear operator T = TΩ satisfies the self-adjointness relation
for u, v in H.
Thus A = T2 is a compact self-adjont linear operator on H with
so that A is a positive operator. By the spectral theorem for compact self-adjoint operators, there is an orthonormal basis un of H consisting of eigenvectors of A:
where μn is non-negative by the positivity of A. Hence
with λn ≥ 0. Since T commutes with A, it leaves its eigenspaces invariant. The positivity relation shows that it acts trivially on the zero eigenspace. The other non-zero eigenspaces are all finite-dimensional and mutually orthogonal. Thus an orthonormal basis can be chosen on each eigenspace so that:
(Note that 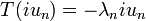 by antilinearity of T.)
by antilinearity of T.)
The non-zero λn (or sometimes their reciprocals) are called the Fredholm eigenvalues of Ω:
If Ω is a bounded domain that is not a disk, Ahlfors showed that
The Fredholm determinant for the domain Ω is defined by[6][7]
Note that this makes sense because A = T2 is a trace class operator.
Schiffer & Hawley (1962) showed that. if 0 lies in Ω and f fixes 0, then[8][9]
Here the norms are in the Bergman spaces of D and its complement Dc and g is a univalent map from Dc onto Ωc fixing ∞.
A similar formula applies in the case of a pair of univalent functions (see below).
Singular integral operators on a closed curve
Let Ω be a bounded simply connected domain in C with smooth boundary C = ∂Ω. Thus there is a univalent holomorphic map f from the unit disk D onto Ω extending to a smooth map between the boundaries S1 and C.
Notes
- ↑ Duren 1983, pp. 131–133
- ↑ Koepf 2007
- ↑ Duren 1983, pp. 143–144
- ↑ Apart from the elementary proof of this result presented here, there are several other analytic proofs in the literature. Nikolski (2002, p. 220), following de Branges, notes that it is a consequence of standard inequalities connected with reproducing kernels. Widom (1988) observed that it was an immediate consequence of Szegő's limit formula (1951). Indeed if f is the real-valued trigonometric polynomial on the circle given as twice the real part of a polynomial g(z) vanishing at 0 on the unit disk, Szegő's limit formula states that the Toeplitz determinants of ef increase to eA where A is the area of g(D). The first determinant is by definition just the constant term in ef = |eg|2.
- ↑ Ahlfors 1966
- ↑ Schiffer 1959, p. 261
- ↑ Schiffer & Hawley 1962, p. 246
- ↑ Schiffer & Hawley 1962, pp. 245–246
- ↑ Takhtajan & Teo 2006
References
- Ahlfors, Lars V. (1952), "Remarks on the Neumann-Poincaré integral equation", Pacific J. Math. 2: 271–280, doi:10.2140/pjm.1952.2.271
- Ahlfors, Lars V. (1966), Lectures on quasiconformal mappings, Van Nostrand
- Ahlfors, Lars V. (2010), Conformal invariants. Topics in geometric function theory. Reprint of the 1973 original. With a foreword by Peter Duren, F. W. Gehring and Brad Osgood, AMS Chelsea Publishing, ISBN 978-0-8218-5270-5
- Astala, Kari; Iwaniec, Tadeusz; Martin, Gaven (2009), Elliptic partial differential equations and quasiconformal mappings in the plane, Princeton mathematical series 48, Princeton University Press, ISBN 0-691-13777-3
- Baranov, A.; Hedenmalm, H. (2008), "Boundary properties of Green functions in the plane", Duke Math. J. 145: 1–24, doi:10.1215/00127094-2008-044
- Bell, S. R. (1992), The Cauchy transform, potential theory, and conformal mapping, Studies in Advanced Mathematics, CRC Press, ISBN 0-8493-8270-X
- Bergman, S.; Schiffer, M. (1951), "Kernel functions and conformal mapping", Compositio Mathematica 8: 205–249
- Duren, P. L. (1983), Univalent functions, Grundlehren der Mathematischen Wissenschaften 259, Springer-Verlag, ISBN 0-387-90795-5
- Gakhov, F. D. (1990), Boundary value problems. Reprint of the 1966 translation, Dover Publications, ISBN 0-486-66275-6
- Garnett, J. B. (2007), Bounded analytic functions, Graduate Texts in Mathematics 236, Springer, ISBN 978-0-387-33621-3
- Goluzin, G. M. (1969), Geometric theory of functions of a complex variable, Translations of Mathematical Monographs 26, American Mathematical Society
- Gong, Sheng (1999), The Bieberbach conjecture, AMS/IP Studies in Advanced Mathematics 12, American Mathematical Society, ISBN 0-8218-0655-6
- Grunsky, Helmut (1939), "Koeffizientenbedingungen für schlicht abbildende meromorphe Funktionen", Mathematische Zeitschrift 45 (1): 29–61, doi:10.1007/BF01580272, ISSN 0025-5874
- Grunsky, Helmut (1978), Lectures on theory of functions in multiply connected domains, Studia Mathematica 4, Vandenhoeck & Ruprecht, ISBN 3-525-40142-6\pages=87–106
- Khavinson, D.; Putinar, M.; Shapiro, H. S. (2007), "Poincaré's variational problem in potential theory", Arch. Ration. Mech. Anal. 185: 143–184, doi:10.1007/s00205-006-0045-1
- Koepf, W. (2007), "Bieberbach’s conjecture, the de Branges and Weinstein functions and the Askey-Gasper inequality", The Ramanujan Journal 13: 103–129, doi:10.1007/s11139-006-0244-2
- Milin, I. M. (1977), Univalent functions and orthonormal systems, Translations of Mathematical Monographs 49, American Mathematical Society
- Neretin, Y. A. (1996), Categories of symmetries and infinite-dimensional groups, London Mathematical Society Monographs 16, Oxford University Press, ISBN 0-19-851186-8
- Nikolski, N. K. (2002), Operators, functions, and systems: an easy reading, Vol. 1: Hardy, Hankel, and Toeplitz, Mathematical Surveys and Monographs 92, American Mathematical Society, ISBN 0-8218-1083-9
- Pommerenke, C. (1975), Univalent functions, with a chapter on quadratic differentials by Gerd Jensen, Studia Mathematica/Mathematische Lehrbücher 15, Vandenhoeck & Ruprecht
- Schiffer, M. (1957), "The Fredholm eigenvalues of plane domains", Pacific J. Math. 7: 1187–1225, doi:10.2140/pjm.1957.7.1187
- Schiffer, M. (1959), "Fredholm eigenvalues of multiply connected domains", Pacific J. Math. 9: 211–269, doi:10.2140/pjm.1959.9.211
- Schiffer, M.; Hawley, N. S. (1962), "Connections and conformal mapping", Acta Math. 107: 175–274, doi:10.1007/bf02545790
- Schiffer, M. (1981), "Fredholm eigenvalues and Grunsky matrices", Ann. Polon. Math. 39: 149–164
- Shapiro, H. S. (1992), The Schwarz function and its generalization to higher dimensions, University of Arkansas Lecture Notes in the Mathematical Sciences 9, Wiley-Interscience, ISBN 0-471-57127-X
- Takhtajan, Leon A.; Teo, Lee-Peng (2006), "Weil–Petersson metric on the universal Teichmüller space", Mem. Amer. Math. Soc. 183
- Widom, H. (1988), "On an inequality of Osgood, Phillips and Sarnak", Proc. Amer. Math. Soc. 102: 773–774, doi:10.1090/s0002-9939-1988-0929019-3
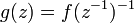
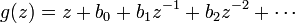
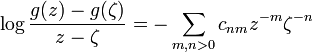
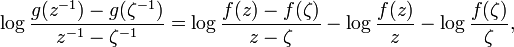
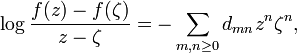
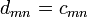
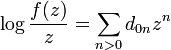
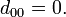
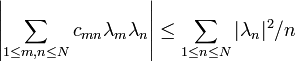
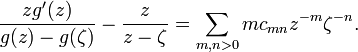
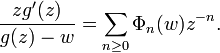
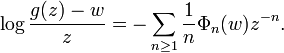
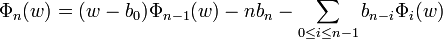
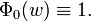
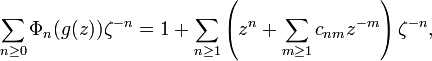
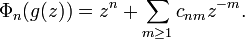
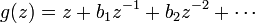
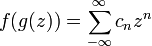
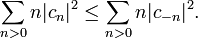
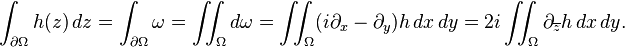
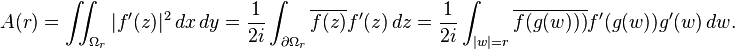
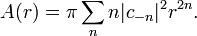
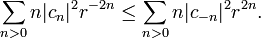
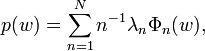
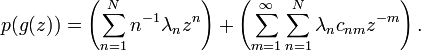
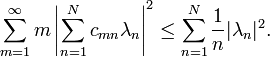
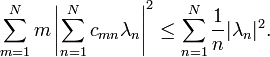
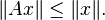
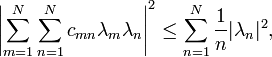
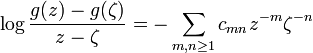
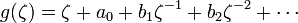
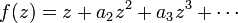
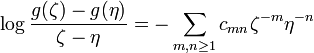
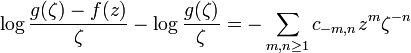
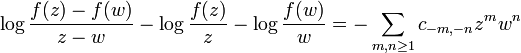
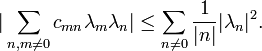
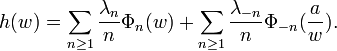
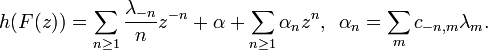
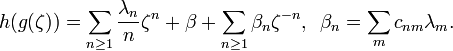
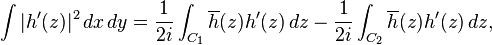
![{1 \over \pi}\iint |h^\prime|^2 \, dx \, dy = \left[\sum_{n\ge 1} {1\over n} |\lambda_{-n}|^2 - \sum_{n\ge 1} |\alpha_n|^2 r^{2n}\right] +\left[\sum_{n\ge 1}{1\over n}|\lambda_n|^2 - \sum_{n\ge 1} |\beta_n|^2 R^{-2n}\right].](../I/m/c606f0a24d169bfa288bb07352871bae.png)
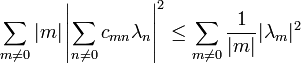
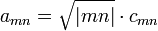
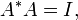
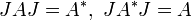
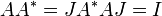
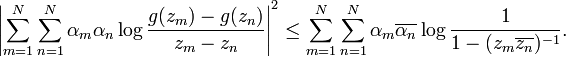
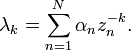
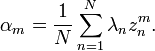
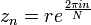
![\left|\sum_{m=1}^N \sum_{n=1}^N \alpha_m \alpha_n\left[ {f^\prime(z_m)f^\prime(z_n) \over(f(z_m)-f(z_n))^2} - {1\over (z_m-z_n)^{2}}\right] \right| \le \sum_{m=1}^N \sum_{n=1}^N \alpha_m\overline{\alpha_n} {1\over (1-z_m\overline{z_n})^2}.](../I/m/30a87b70f6b3905661865b42f48bdfa3.png)
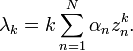
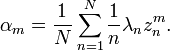
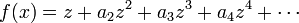
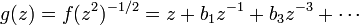
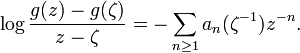
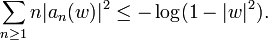
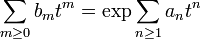
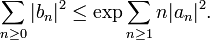
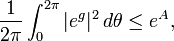
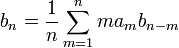
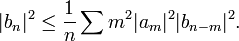
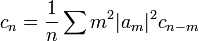
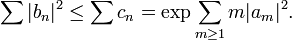
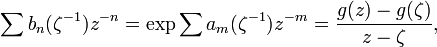
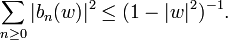
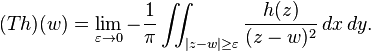
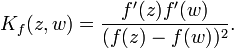
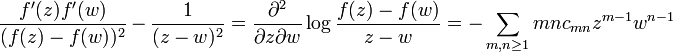
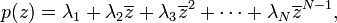
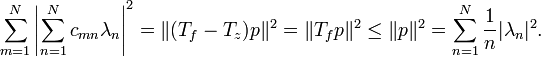
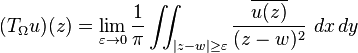
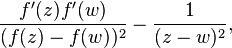
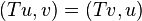
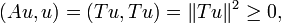
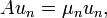
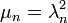
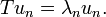
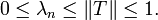
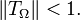
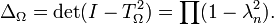
![\Delta_\Omega= -{1\over 12\pi}\left[\|\partial_z \log f^\prime\|^2_D +\|\partial_z \log g^\prime\|^2_{D^c} - 2 \|\partial_z\log f(z)/z \|^2_D - 2 \|\partial_z\log g(z)/z \|^2_{D^c}\right].](../I/m/2b45207c2cb916d193a6286b3d2b526a.png)