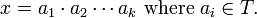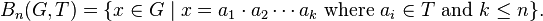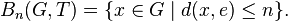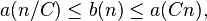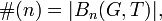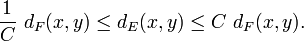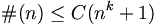Growth rate (group theory)
In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length n.
Definition
Suppose G is a finitely generated group; and T is a finite symmetric set of generators
(symmetric means that if 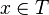 then
then 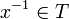 ).
Any element
).
Any element 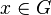 can be expressed as a word in the T-alphabet
can be expressed as a word in the T-alphabet
Let us consider the subset of all elements of G which can be presented by such a word of length ≤ n
This set is just the closed ball of radius n in the word metric d on G with respect to the generating set T:
More geometrically, 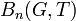 is the set of vertices in the Cayley graph with respect to T which are within distance n of the identity.
is the set of vertices in the Cayley graph with respect to T which are within distance n of the identity.
Given two nondecreasing positive functions a and b one can say that
they are equivalent (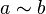 ) if there is a constant C such that
) if there is a constant C such that
for example 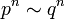 if
if 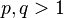 .
.
Then the growth rate of the group G can be defined as the corresponding equivalence class of the function
where 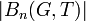 denotes the number of elements in the set
denotes the number of elements in the set 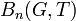 .
Although the function
.
Although the function 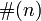 depends on the set of generators T its rate of
growth does not (see below) and therefore the rate of growth gives an invariant of a group.
depends on the set of generators T its rate of
growth does not (see below) and therefore the rate of growth gives an invariant of a group.
The word metric d and therefore sets 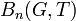 depend
on the generating set T. However, any two such metrics are bilipschitz equivalent in the following sense: for finite symmetric generating sets E, F, there is a positive constant C such that
depend
on the generating set T. However, any two such metrics are bilipschitz equivalent in the following sense: for finite symmetric generating sets E, F, there is a positive constant C such that
As an immediate corollary of this inequality we get that the growth rate does not depend on the choice of generating set.
Polynomial and exponential growth
If
for some 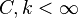 we say that G has a polynomial growth rate.
The infimum
we say that G has a polynomial growth rate.
The infimum 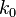 of such k's is called the order of polynomial growth.
According to Gromov's theorem, a group of polynomial growth is virtually nilpotent, i.e. it has a nilpotent subgroup of finite index. In particular, the order of polynomial growth
of such k's is called the order of polynomial growth.
According to Gromov's theorem, a group of polynomial growth is virtually nilpotent, i.e. it has a nilpotent subgroup of finite index. In particular, the order of polynomial growth 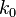 has to be a natural number and in fact
has to be a natural number and in fact 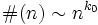 .
.
If 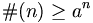 for some
for some 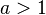 we say that G has an exponential growth rate.
Every finitely generated G has at most exponential growth, i.e. for some
we say that G has an exponential growth rate.
Every finitely generated G has at most exponential growth, i.e. for some 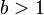 we have
we have 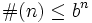 .
.
If 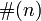 grows more slowly than any exponential function, G has a subexponential growth rate. Any such group is amenable.
grows more slowly than any exponential function, G has a subexponential growth rate. Any such group is amenable.
Examples
- A free group with a finite rank k > 1 has an exponential growth rate.
- A finite group has constant growth – polynomial growth of order 0 – and includes fundamental groups of manifolds whose universal cover is compact.
- If M is a closed negatively curved Riemannian manifold then its fundamental group
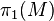 has exponential growth rate. Milnor proved this using the fact that the word metric on
has exponential growth rate. Milnor proved this using the fact that the word metric on 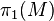 is quasi-isometric to the universal cover of M.
is quasi-isometric to the universal cover of M.
- Zd has a polynomial growth rate of order d.
- The discrete Heisenberg group H3 has a polynomial growth rate of order 4. This fact is a special case of the general theorem of Bass and Guivarch that is discussed in the article on Gromov's theorem.
- The lamplighter group has an exponential growth.
- The existence of groups with intermediate growth, i.e. subexponential but not polynomial was open for many years. It was asked by Milnor in 1968 and was finally answered in the positive by Grigorchuk in 1984. There are still open questions in this area and a complete picture of which orders of growth are possible and which are not is missing.
- The triangle groups include 3 finite groups (the spherical ones, corresponding to sphere), 3 groups of quadratic growth (the Euclidean ones, corresponding to Euclidean plane), and infinitely many groups of exponential growth (the hyperbolic ones, corresponding to the hyperbolic plane).
See also
References
- J. Milnor, A note on curvature and fundamental group, J. Differential Geometry 2 (1968), 1–7.
- R. I. Grigorchuk, Degrees of growth of finitely generated groups and the theory of invariant means., Izv. Akad. Nauk SSSR Ser. Mat. 48:5 (1984), 939–985 (Russian).
Further reading
- Rostislav Grigorchuk and Igor Pak (2006). "Groups of Intermediate Growth: an Introduction for Beginners". arXiv:math.GR/0607384.