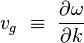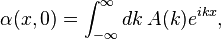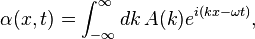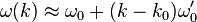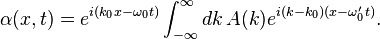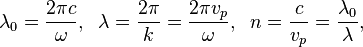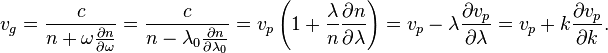Group velocity

This shows a wave with the group velocity and phase velocity going in different directions.[1] The group velocity is positive (i.e. the envelope of the wave moves rightward), while the phase velocity is negative (i.e. the peaks and troughs move leftward).

The group velocity of a wave is the velocity with which the overall shape of the waves' amplitudes—known as the modulation or envelope of the wave—propagates through space.

For example, if a stone is thrown into the middle of a very still pond, a circular pattern of waves with a quiescent center appears in the water. The expanding ring of waves is the wave group, within which one can discern individual wavelets of differing wavelengths traveling at different speeds. The longer waves travel faster than the group as a whole, but their amplitudes diminish as they approach the leading edge. The shorter waves travel more slowly, and their amplitudes diminish as they emerge from the trailing boundary of the group.

Definition and interpretation

Definition

Solid line: A wave packet. Dashed line: The envelope of the wave packet. The envelope moves at the group velocity.

The group velocity vg is defined by the equation:[2][3][4][5]

v_g \ \equiv\ \frac{\partial \omega}{\partial k}\,

where ω is the wave's angular frequency (usually expressed in radians per second), and k is the angular wavenumber (usually expressed in radians per meter).

The function ω(k), which gives ω as a function of k, is known as the dispersion relation.

Derivation

One derivation of the formula for group velocity is as follows.[6][7]

Consider a wave packet as a function of position x and time t: α(x,t). Let A(k) be its Fourier transform at time t=0:

\alpha(x,0)= \int_{-\infty}^\infty dk \, A(k) e^{ikx},

By the superposition principle, the wavepacket at any time t is:

\alpha(x,t)= \int_{-\infty}^\infty dk \, A(k) e^{i(kx-\omega t)},

where ω is implicitly a function of k. We assume that the wave packet α is almost monochromatic, so that A(k) is sharply peaked around a central wavenumber k0. Then, linearization gives:

\omega(k) \approx \omega_0 + (k-k_0)\omega'_0

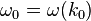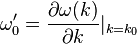where \omega_0=\omega(k_0) and \omega'_0=\frac{\partial \omega(k)}{\partial k} |_{k=k_0} (see next section for discussion of this step). Then, after some algebra,

\alpha(x,t)= e^{i(k_0 x - \omega_0 t)}\int_{-\infty}^\infty dk \, A(k) e^{i(k-k_0)(x-\omega'_0 t)}.

There are two factors in this expression. The first factor, 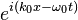e^{i(k_0 x - \omega_0 t)}, describes a perfect monochromatic wave with wavevector 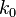k_0, with peaks and troughs moving at the phase velocity 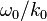\omega_0/k_0 within the envelope of the wavepacket. The other factor, 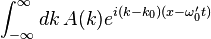\int_{-\infty}^\infty dk \, A(k) e^{i(k-k_0)(x-\omega'_0 t)}, gives the envelope of the wavepacket. This envelope function depends on position and time only through the combination 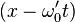(x-\omega'_0 t). Therefore, the envelope of the wavepacket travels at velocity 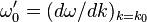\omega'_0=(d\omega/dk)_{k=k_0}. This explains the group velocity formula.

Higher-order terms in dispersion

Distortion of wave groups by higher-order dispersion effects, for surface gravity waves on deep water (with vg = ½vp). The superposition of three wave components – with respectively 22, 25 and 29 meter wavelengths, fitting in a periodic horizontal domain of 2 km length – is shown. The wave amplitudes of the components are respectively 1, 2 and 1 meter.

Part of the previous derivation is the assumption:

\omega(k) \approx \omega_0 + (k-k_0)\omega'_0

If the wavepacket has a relatively large frequency spread, or if the dispersion 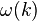\omega(k) has sharp variations (such as due to a resonance), or if the packet travels over very long distances, this assumption is not valid. As a result, the envelope of the wave packet not only moves, but also distorts. Loosely speaking, different frequency-components of the wavepacket travel at different speeds, with the faster components moving towards the front of the wavepacket and the slower moving towards the back. Eventually, the wave packet gets stretched out.

The next-higher term in the Taylor series (related to the second derivative of 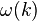\omega(k)) is called group velocity dispersion. This is an important effect in the propagation of signals through optical fibers and in the design of high-power, short-pulse lasers.

Physical interpretation

The group velocity is often thought of as the velocity at which energy or information is conveyed along a wave. In most cases this is accurate, and the group velocity can be thought of as the signal velocity of the waveform. However, if the wave is travelling through an absorptive medium, this does not always hold. Since the 1980s, various experiments have verified that it is possible for the group velocity of laser light pulses sent through specially prepared materials to significantly exceed the speed of light in vacuum. However, superluminal communication is not possible in this case, since the signal velocity remains less than the speed of light. It is also possible to reduce the group velocity to zero, stopping the pulse, or have negative group velocity, making the pulse appear to propagate backwards.[1] However, in all these cases, photons continue to propagate at the expected speed of light in the medium.[8][9][10][11]

Anomalous dispersion happens in areas of rapid spectral variation with respect to the refractive index. Therefore, negative values of the group velocity will occur in these areas. Anomalous dispersion plays a fundamental role in achieving backward propagating and superluminal light. Anomalous dispersion can also be used to produce group and phase velocities that are in different directions.[9] Materials that exhibit large anomalous dispersion allow the group velocity of the light to exceed c and/or become negative.[11][12]

History

The idea of a group velocity distinct from a wave's phase velocity was first proposed by W.R. Hamilton in 1839, and the first full treatment was by Rayleigh in his "Theory of Sound" in 1877.[13]

Other expressions

For light, the refractive index n, vacuum wavelength λ0, and wavelength in the medium λ, are related by

\lambda_0=\frac{2\pi c}{\omega}, \;\; \lambda = \frac{2\pi}{k} = \frac{2\pi v_p}{\omega}, \;\; n=\frac{c}{v_p}=\frac{\lambda_0}{\lambda},

with vp = ω/k the phase velocity.

The group velocity, therefore, can be calculated by any of the following formulas:

v_g = \frac{c}{n + \omega \frac{\partial n}{\partial \omega}} = \frac{c}{n - \lambda_0 \frac{\partial n}{\partial \lambda_0}} = v_p \left( 1+\frac{\lambda}{n} \frac{\partial n}{\partial \lambda} \right) = v_p - \lambda \frac{\partial v_p}{\partial \lambda} = v_p + k \frac{\partial v_p}{\partial k}.

In three dimensions

See also: Plane wave

For waves traveling through three dimensions, such as light waves, sound waves, and matter waves, the formulas for phase and group velocity are generalized in a straightforward way:[14]

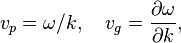
One dimension: v_p = \omega/k, \quad v_g = \frac{\partial \omega}{\partial k}, \,
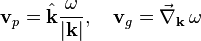
Three dimensions: \mathbf{v}_p = \hat{\mathbf{k}} \frac{\omega}{|\mathbf{k}|}, \quad \mathbf{v}_g = \vec{\nabla}_{\mathbf{k}} \, \omega \,

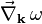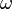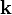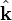where \vec{\nabla}_{\mathbf{k}} \, \omega means the gradient of the angular frequency \omega as a function of the wave vector \mathbf{k}, and \hat{\mathbf{k}} is the unit vector in direction k.

If the waves are propagating through an anisotropic (i.e., not rotationally symmetric) medium, for example a crystal, then the phase velocity vector and group velocity vector may point in different directions.

See also

References

Notes

  1. ↑ 1.0 1.1 Nemirovsky, Jonathan; Rechtsman, Mikael C and Segev, Mordechai (9 April 2012). "Negative radiation pressure and negative effective refractive index via dielectric birefringence" (PDF). Optics Express 20 (8): 8907–8914. Bibcode:2012OExpr..20.8907N. doi:10.1364/OE.20.008907. PMID 22513601.
  2. ↑ Brillouin, Léon (2003) [1946], Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices, Dover, p. 75, ISBN 978-0-486-49556-9
  3. ↑ Lighthill, James (2001) [1978], Waves in fluids, Cambridge University Press, p. 242, ISBN 978-0-521-01045-0
  4. ↑ Lighthill (1965)
  5. ↑ Hayes (1973)
  6. ↑ Griffiths, David J. (1995). Introduction to Quantum Mechanics. Prentice Hall. p. 48.
  7. ↑ David K. Ferry (2001). Quantum Mechanics: An Introduction for Device Physicists and Electrical Engineers (2nd ed.). CRC Press. pp. 18–19. ISBN 978-0-7503-0725-3.
  8. ↑ Gehring, George M.; Schweinsberg, Aaron; Barsi, Christopher; Kostinski, Natalie; Boyd, Robert W. (2006), "Observation of a Backward Pulse Propagation Through a Medium with a Negative Group Velocity", Science 312 (5775): 895–897, Bibcode:2006Sci...312..895G, doi:10.1126/science.1124524, PMID 16690861
  9. ↑ 9.0 9.1 Dolling, Gunnar; Enkrich, Christian; Wegener, Martin; Soukoulis, Costas M.; Linden, Stefan (2006), "Simultaneous Negative Phase and Group Velocity of Light in a Metamaterial", Science 312 (5775): 892–894, Bibcode:2006Sci...312..892D, doi:10.1126/science.1126021, PMID 16690860
  10. ↑ Schweinsberg, A.; Lepeshkin, N. N.; Bigelow, M.S.; Boyd, R. W.; Jarabo, S. (2005), "Observation of superluminal and slow light propagation in erbium-doped optical fiber", Europhysics Letters 73 (2): 218–224, Bibcode:2006EL.....73..218S, doi:10.1209/epl/i2005-10371-0
  11. ↑ 11.0 11.1 Bigelow, Matthew S.; Lepeshkin, Nick N.; Shin, Heedeuk; Boyd, Robert W. (2006), "Propagation of a smooth and discontinuous pulses through materials with very large or very small group velocities", Journal of Physics: Condensed Matter 18 (11): 3117–3126, Bibcode:2006JPCM...18.3117B, doi:10.1088/0953-8984/18/11/017
  12. ↑ Withayachumnankul, W.; Fischer, B. M.; Ferguson, B.; Davis, B. R.; Abbott, D. (2010), "A Systemized View of Superluminal Wave Propagation", Proceedings of the IEEE 98 (10): 1775–1786, doi:10.1109/JPROC.2010.2052910
  13. ↑ Brillouin, Léon (1960), Wave Propagation and Group Velocity, New York: Academic Press Inc., OCLC 537250
  14. ↑ Atmospheric and oceanic fluid dynamics: fundamentals and large-scale circulation, by Geoffrey K. Vallis, p239
  15. ↑ http://www.rp-photonics.com/group_delay.html

Further reading

  • Tipler, Paul A.; Llewellyn, Ralph A. (2003), Modern Physics (4th ed.), New York: W. H. Freeman and Company, p. 223, ISBN 0-7167-4345-0.
  • Biot, M. A. (1957), "General theorems on the equivalence of group velocity and energy transport", Physical Review 105 (4): 1129–1137, Bibcode:1957PhRv..105.1129B, doi:10.1103/PhysRev.105.1129
  • Whitham, G. B. (1961), "Group velocity and energy propagation for three-dimensional waves", Communications on Pure and Applied Mathematics 14 (3): 675–691, doi:10.1002/cpa.3160140337
  • Lighthill, M. J. (1965), "Group velocity", IMA Journal of Applied Mathematics 1 (1): 1–28, doi:10.1093/imamat/1.1.1
  • Bretherton, F. P.; Garrett, C. J. R. (1968), "Wavetrains in inhomogeneous moving media", Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences 302 (1471): 529–554, Bibcode:1968RSPSA.302..529B, doi:10.1098/rspa.1968.0034
  • Hayes, W. D. (1973), "Group velocity and nonlinear dispersive wave propagation", Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences 332 (1589): 199–221, Bibcode:1973RSPSA.332..199H, doi:10.1098/rspa.1973.0021
  • Whitham, G. B. (1974), Linear and nonlinear waves, Wiley, ISBN 0471940909

External links


Velocities of waves
Phase velocity • Group velocity • Front velocity • Signal velocity