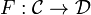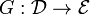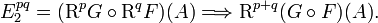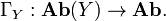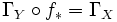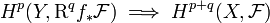Grothendieck spectral sequence

In mathematics, in the field of homological algebra, the Grothendieck spectral sequence is a spectral sequence that computes the derived functors of the composition of two functors $G\circ F$ , from knowledge of the derived functors of F and G.

F :\mathcal{C}\to\mathcal{D}

and

G :\mathcal{D}\to\mathcal{E}

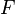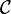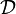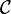are two additive and left exact(covariant) functors between abelian categories such that $F$ takes injective objects of $\mathcal{C}$ to $G$ -acyclic objects of $\mathcal{D}$ , then there is a spectral sequence for each object $A$ of $\mathcal{C}$ :

E_2^{pq} = ({\rm R}^p G \circ{\rm R}^q F)(A) \Longrightarrow {\rm R}^{p+q} (G\circ F)(A).

Many spectral sequences are instances of the Grothendieck spectral sequence, for example the Leray spectral sequence.

The exact sequence of low degrees reads

0 → R¹G(FA) → R¹(GF)(A) → G(R¹F(A)) → R²G(FA) → R²(GF)(A).

Example: the Leray spectral sequence

If $X$ and $Y$ are topological spaces, let

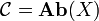\mathcal{C} = \mathbf{Ab}(X)

and

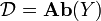\mathcal{D} = \mathbf{Ab}(Y)

be the category of sheaves of abelian groups on X and Y, respectively and

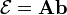\mathcal{E} = \mathbf{Ab}

be the category of abelian groups.

For a continuous map

f : X \to Y

there is the (left-exact) direct image functor

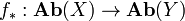f_* : \mathbf{Ab}(X) \to \mathbf{Ab}(Y)

We also have the global section functors

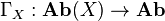\Gamma_X : \mathbf{Ab}(X)\to \mathbf{Ab}

and

\Gamma_Y : \mathbf{Ab}(Y) \to \mathbf {Ab}.

Then since

\Gamma_Y \circ f_* = \Gamma_X

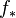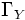and the functors $f_*$ and $\Gamma_Y$ satisfy the hypotheses (since the direct image functor has an exact left adjoint 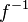$f^{-1}$ , pushforwards of injectives are injective and in particular acyclic for the global section functor), the sequence in this case becomes:

H^p(Y,{\rm R}^q f_*\mathcal{F})\implies H^{p+q}(X,\mathcal{F})

for a sheaf $\mathcal{F}$ of abelian groups on $X$ , and this is exactly the Leray spectral sequence.

References

Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR 1269324

This article incorporates material from Grothendieck spectral sequence on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.