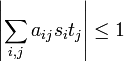Grothendieck inequality

In mathematics, the Grothendieck inequality states that there is a universal constant k with the following property. If ai,j is an n by n (real or complex) matrix with

\left| \sum_{i,j} a_{ij} s_i t_j \right|\le 1

for all (real or complex) numbers si, tj of absolute value at most 1, then

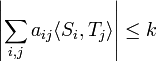\left| \sum_{i,j} a_{ij} \langle S_i , T_j \rangle \right|\le k,

for all vectors Si, Tj in the unit ball B(H) of a (real or complex) Hilbert space H. The smallest constant k which satisfies this property for all n by n matrices is called a Grothendieck constant and denoted k(n). In fact there are two Grothendieck constants kR(n) and kC(n) for each n depending on whether one works with real or complex numbers, respectively.[1]

The Grothendieck inequality and Grothendieck constants are named after Alexander Grothendieck, who proved the inequality and the existence of the constants in a paper published in 1953.[2]

Bounds on the constants

The sequences kR(n) and kC(n) are easily seen to be increasing, and Grothendieck's result states that they are bounded,[2][3] so they have limits.

With kR defined to be supn kR(n)[4] then Grothendieck proved that: 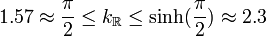1.57 \approx \frac{\pi}{2} \leq k_{\R} \leq \mathrm{sinh}(\frac{\pi}{2}) \approx 2.3.

Krivine (1979)[5] improved the result by proving: 1.67696... ≤ kR ≤ 1.7822139781...=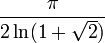 \frac{\pi}{2 \ln(1+\sqrt{2})}, conjecturing that the upper bound is tight. However, this conjecture was disproved by Braverman et al. (2011).[6]

See also

References

  1. ↑ Pisier, Gilles (April 2012), "Grothendieck's Theorem, Past and Present", Bulletin of the American Mathematical Society 49 (2): 237–323, doi:10.1090/S0273-0979-2011-01348-9.
  2. ↑ 2.0 2.1 Grothendieck, Alexander (1953), "Résumé de la théorie métrique des produits tensoriels topologiques", Bol. Soc. Mat. Sao Paulo 8: 1–79, MR 0094682
  3. ↑ Blei, Ron C. (1987), "An elementary proof of the Grothendieck inequality", Proceedings of the American Mathematical Society (American Mathematical Society) 100 (1): 58–60, doi:10.2307/2046119, ISSN 0002-9939, JSTOR 2046119, MR 883401
  4. ↑ Finch, Steven R. (2003), Mathematical constants, Cambridge University Press, ISBN 978-0-521-81805-6
  5. ↑ Krivine, J.-L. (1979), "Constantes de Grothendieck et fonctions de type positif sur les sphères", Advances in Mathematics 31 (1): 16–30, doi:10.1016/0001-8708(79)90017-3, ISSN 0001-8708, MR 521464
  6. ↑ Braverman, Mark; Makarychev, Konstantin; Makarychev, Yury; Naor, Assaf (2011), "The Grothendieck Constant is Strictly Smaller than Krivine's Bound", 52nd Annual IEEE Symposium on Foundations of Computer Science (FOCS), pp. 453–462, arXiv:1103.6161, doi:10.1109/FOCS.2011.77

External links