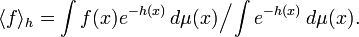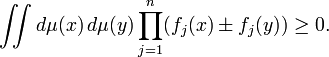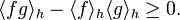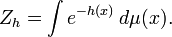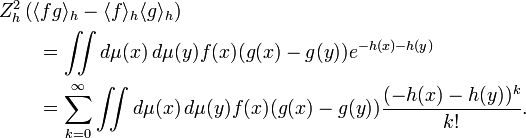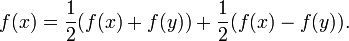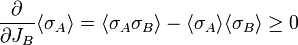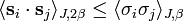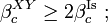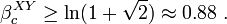Griffiths inequality
In statistical mechanics, the Griffiths inequality, sometimes also called Griffiths–Kelly–Sherman inequality or GKS inequality, named after Robert B. Griffiths, is a correlation inequality for ferromagnetic spin systems. Informally, it says that in ferromagnetic spin systems, if the 'a-priori distribution' of the spin is invariant under spin flipping, the correlation of any monomial of the spins is non-negative; and the two point correlation of two monomial of the spins is non-negative.
The inequality was proved by Griffiths for Ising ferromagnets with two-body interactions,[1] then generalised by Kelly and Sherman to interactions involving an arbitrary number of spins,[2] and then by Griffiths to systems with arbitrary spins.[3] A more general formulation was given by Ginibre,[4] and is now called the Ginibre inequality.
Definitions
Let 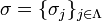 be a configuration of (continuous or discrete) spins on a lattice Λ. If A ⊂ Λ is a list of lattice sites, possibly with duplicates, let
be a configuration of (continuous or discrete) spins on a lattice Λ. If A ⊂ Λ is a list of lattice sites, possibly with duplicates, let 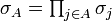 be the product of the spins in A.
be the product of the spins in A.
Assign an a-priori measure dμ(σ) on the spins; let H be an energy functional of the form
where the sum is over lists of sites A, and let
be the partition function. As usual,
stands for the ensemble average.
The system is called ferromagnetic if, for any list of sites A, JA ≥ 0. The system is called invariant under spin flipping if, for any j in Λ, the measure μ is preserved under the sign flipping map σ → τ, where
Statement of inequalities
First Griffiths inequality
In a ferromagnetic spin system which is invariant under spin flipping,
for any list of spins A.
Second Griffiths inequality
In a ferromagnetic spin system which is invariant under spin flipping,
for any lists of spins A and B.
The first inequality is a special case of the second one, corresponding to B = ∅.
Proof
Observe that the partition function is non-negative by definition.
Proof of first inequality: Expand
then
where nA(j) stands for the number of times that j appears in A. Now, by invariance under spin flipping,
if at least one n(j) is odd, and the same expression is obviously non-negative for even values of n. Therefore Z<σA>≥0, hence also <σA>≥0.
Proof of second inequality. For the second Griffiths inequality, double the random variable, i.e. consider a second copy of the spin, 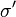 , with the same distribution of
, with the same distribution of  . Then
. Then
Introduce the new variables
The doubled system  is ferromagnetic in
is ferromagnetic in 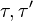 because
because 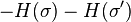 is a polynomial in
is a polynomial in 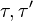 with positive coefficients
with positive coefficients
Besides the measure on 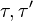 is invariant under spin flipping because
is invariant under spin flipping because 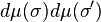 is.
Finally the monomials
is.
Finally the monomials 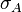 ,
, 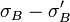 are polynomials in
are polynomials in 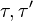 with positive coefficients
with positive coefficients
The first Griffiths inequality applied to 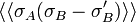 gives the result.
gives the result.
More details are in.[5]
Extension: Ginibre inequality
The Ginibre inequality is an extension, found by Jean Ginibre,[4] of the Griffiths inequality.
Formulation
Let (Γ, μ) be a probability space. For functions f, h on Γ, denote
Let A be a set of real functions on Γ such that. for every f1,f2,...,fn in A, and for any choice of signs ±,
Then, for any f,g,−h in the convex cone generated by A,
Proof
Let
Then
Now the inequality follows from the assumption and from the identity
Examples
- To recover the (second) Griffiths inequality, take Γ = {−1, +1}Λ, where Λ is a lattice, and let μ be a measure on Γ that is invariant under sign flipping. The cone A of polynomials with positive coefficients satisfies the assumptions of the Ginibre inequality.
- (Γ, μ) is a commutative compact group with the Haar measure, A is the cone of real positive definite functions on Γ.
- Γ is a totally ordered set, A is the cone of real positive non-decreasing functions on Γ. This yields Chebyshev's sum inequality. For extension to partially ordered sets, see FKG inequality.
Applications
- The thermodynamic limit of the correlations of the ferromagnetic Ising model (with non-negative external field h and free boundary conditions) exists.
- This is because increasing the volume is the same as switching on new couplings JB for a certain subset B. By the second Griffiths inequality
- Hence
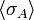 is monotonically increasing with the volume; then it converges since it is bounded by 1.
is monotonically increasing with the volume; then it converges since it is bounded by 1.
- The one-dimensional, ferromagnetic Ising model with interactions
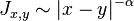 displays a phase transition if
displays a phase transition if 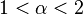 .
.
- This property can be showed in a hierarchical approximation, that differs from the full model by the absence of some interactions: arguing as above with the second Griffiths inequality, the results carries over the full model.[6]
- The Ginibre inequality provides the existence of the thermodynamic limit for the free energy and spin correlations for the two-dimensional classical XY model.[4] Besides, through Ginibre inequality, Kunz and Pfister proved the presence of a phase transition for the ferromagnetic XY model with interaction
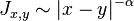 if
if 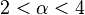 .
.
- Aizenman and Simon[7] used the Ginibre inequality to prove that the two point spin correlation of the ferromagnetic classical XY model in dimension
 , coupling
, coupling 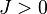 and inverse temperature
and inverse temperature  is dominated by (i.e. has upper bound given by) the two point correlation of the ferromagnetic Ising model in dimension
is dominated by (i.e. has upper bound given by) the two point correlation of the ferromagnetic Ising model in dimension  , coupling
, coupling 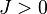 , and inverse temperature
, and inverse temperature 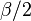
- Hence the critical
 of the XY model cannot be smaller than the double of the critical temperature of the Ising model
of the XY model cannot be smaller than the double of the critical temperature of the Ising model
- in dimension D = 2 and coupling J = 1, this gives
- There exists a version of the Ginibre inequality for the Coulomb gas that implies the existence of thermodynamic limit of correlations.[8]
- Other applications (phase transitions in spin systems, XY model, XYZ quantum chain) are reviewed in.[9]
References
- ↑ Griffiths, R.B. (1967). "Correlations in Ising Ferromagnets. I". J. Math. Phys. 8 (3): 478–483. doi:10.1063/1.1705219.
- ↑ Kelly, D.J.; Sherman, S. (1968). "General Griffiths' inequalities on correlations in Ising ferromagnets". J. Math. Phys. 9: 466. doi:10.1063/1.1664600.
- ↑ Griffiths, R.B. (1969). "Rigorous Results for Ising Ferromagnets of Arbitrary Spin". J. Math. Phys. 10: 1559. doi:10.1063/1.1665005.
- ↑ 4.0 4.1 4.2 Ginibre, J. (1970). "General formulation of Griffiths' inequalities". Comm. Math. Phys. 16 (4): 310–328. doi:10.1007/BF01646537.
- ↑ Glimm, J.; Jaffe, A. (1987). Quantum Physics. A functional integral point of view. New York: Springer-Verlag. ISBN 0-387-96476-2.
- ↑ Dyson, F.J. (1969). "Existence of a phase-transition in a one-dimensional Ising ferromagnet". Comm. Math. Phys. 12: 91–107. doi:10.1007/BF01645907.
- ↑ Aizenman, M.; Simon, B. (1980). "A comparison of plane rotor and Ising models". Phys. Lett. A 76. doi:10.1016/0375-9601(80)90493-4.
- ↑ Fröhlich, J.; Park, Y.M. (1978). "Correlation inequalities and the thermodynamic limit for classical and quantum continuous systems". Comm. Math. Phys. 59 (3): 235–266. doi:10.1007/BF01611505.
- ↑ Griffiths, R.B. (1972). "Rigorous results and theorems". In C. Domb and M.S.Green. Phase Transitions and Critical Phenomena 1. New York: Academic Press. p. 7.
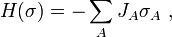
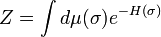
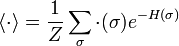
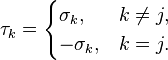
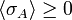
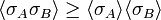
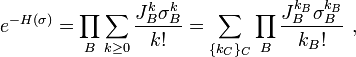
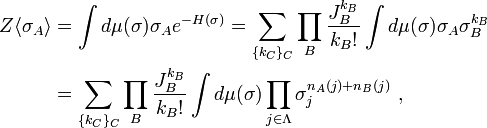
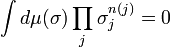
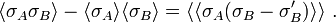

![\begin{align}
\sum_A J_A (\sigma_A+\sigma'_A) &= \sum_A J_A\sum_{X\subset A}
\left[1+(-1)^{|X|}\right] \tau_{A \setminus X} \tau'_X
\end{align}](../I/m/516c9103d89a0245fc7261ca3b88585b.png)
![\begin{align}
\sigma_A &= \sum_{X \subset A} \tau_{A \setminus X} \tau'_{X}~, \\
\sigma_B-\sigma'_B &= \sum_{X\subset B}
\left[1-(-1)^{|X|}\right] \tau_{B \setminus X} \tau'_X~.
\end{align}](../I/m/3e7dd81d61978f2bbab8784d541e5aa3.png)