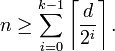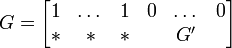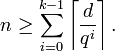Griesmer bound
In the mathematics of coding theory, the Griesmer bound, named after James Hugo Griesmer, is a bound on the length of binary codes of dimension k and minimum distance d. There is also a very similar version for non-binary codes.
Statement of the bound
For a binary linear code, the Griesmer bound says:
Proof
Let 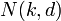 denote the minimum length of a binary code of dimension k and distance d. Let C be such a code.
We want to show that
denote the minimum length of a binary code of dimension k and distance d. Let C be such a code.
We want to show that 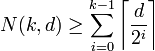 .
.
Let G be a generator matrix of C. We can always suppose that the first row of G is of the form r = (1, ..., 1, 0, ..., 0) with weight d.
The matrix G' generates a code C', which is called the residual code of C.
C' has obviously dimension 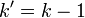 and length
and length 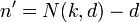 .
C' has a distance d', but we don't know it.
Let
.
C' has a distance d', but we don't know it.
Let 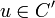 s.t.
s.t. 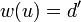 . There exists a vector
. There exists a vector
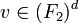 s.t. the concatenation
s.t. the concatenation 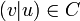 .
Then
.
Then 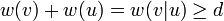 . On the other hand, also
. On the other hand, also 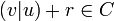 , since
, since 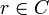 and
and  is linear, so
is linear, so 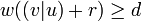 . But
. But
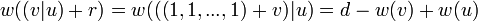 ,
,
so this becomes 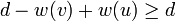 . By summing this with
. By summing this with 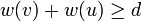 , we obtain
, we obtain 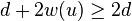 . But
. But 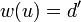 , so we get
, so we get
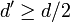 . This implies
. This implies 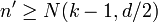 , therefore
, therefore 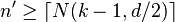 (due to the integrality of n'), so that
(due to the integrality of n'), so that
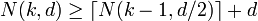 .
By induction over k we will eventually get
.
By induction over k we will eventually get
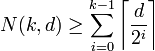 (note that at any step the dimension decreases by 1 and the distance is halved, and we use the identity
(note that at any step the dimension decreases by 1 and the distance is halved, and we use the identity 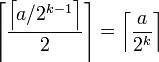 for any integer a and positive integer k).
for any integer a and positive integer k).
The bound for the general case
For a linear code over 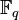 , the Griesmer bound becomes:
, the Griesmer bound becomes:
The proof is similar to the binary case and so it is omitted.
See also
- Singleton bound
- Hamming bound
- Gilbert-Varshamov bound
- Johnson bound
- Plotkin bound
References
- J. H. Griesmer, "A bound for error-correcting codes," IBM Journal of Res. and Dev., vol. 4, no. 5, pp. 532-542, 1960.