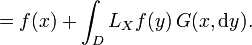Green measure
In mathematics — specifically, in stochastic analysis — the Green measure is a measure associated to an Itō diffusion. There is an associated Green formula representing suitably smooth functions in terms of the Green measure and first exit times of the diffusion. The concepts are named after the British mathematician George Green and are generalizations of the classical Green's function and Green formula to the stochastic case using Dynkin's formula.
Notation
Let X be an Rn-valued Itō diffusion satisfying an Itō stochastic differential equation of the form
Let Px denote the law of X given the initial condition X0 = x, and let Ex denote expectation with respect to Px. Let LX be the infinitesimal generator of X, i.e.
Let D ⊆ Rn be an open, bounded domain; let τD be the first exit time of X from D:
The Green measure
Intuitively, the Green measure of a Borel set H (with respect to a point x and domain D) is the expected length of time that X, having started at x, stays in H before it leaves the domain D. That is, the Green measure of X with respect to D at x, denoted G(x, ·), is defined for Borel sets H ⊆ Rn by
or for bounded, continuous functions f : D → R by
The name "Green measure" comes from the fact that if X is Brownian motion, then
where G(x, y) is Green's function for the operator LX (which, in the case of Brownian motion, is ½Δ, where Δ is the Laplace operator) on the domain D.
The Green formula
Suppose that Ex[τD] < +∞ for all x ∈ D, and let f : Rn → R be of smoothness class C2 with compact support. Then
In particular, for C2 functions f with support compactly embedded in D,
The proof of Green's formula is an easy application of Dynkin's formula and the definition of the Green measure:
References
- Øksendal, Bernt K. (2003). Stochastic Differential Equations: An Introduction with Applications (Sixth edition ed.). Berlin: Springer. ISBN 3-540-04758-1. MR 2001996 (See Section 9)
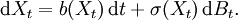
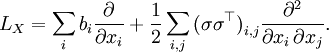
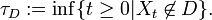
![G(x, H) = \mathbf{E}^{x} \left[ \int_{0}^{\tau_{D}} \chi_{H} (X_{s}) \, \mathrm{d} s \right],](../I/m/79fecafb38eed33c8226c15497f22406.png)
![\int_{D} f(y) \, G(x, \mathrm{d} y) = \mathbf{E}^{x} \left[ \int_{0}^{\tau_{D}} f(X_{s}) \, \mathrm{d} s \right]](../I/m/adbef808a8cc3929f6ef2d040fe1fffb.png)
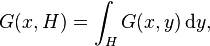
![f(x) = \mathbf{E}^{x} \big[ f \big( X_{\tau_{D}} \big) \big] - \int_{D} L_{X} f (y) \, G(x, \mathrm{d} y).](../I/m/5afcf9b836f7b826556ed683424757d1.png)
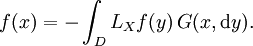
![\mathbf{E}^{x} \big[ f \big( X_{\tau_{D}} \big) \big]](../I/m/6d2282d47ea276e067430e126ff1bac6.png)
![= f(x) + \mathbf{E}^{x} \left[ \int_{0}^{\tau_{D}} L_{X} f (X_{s}) \, \mathrm{d} s \right]](../I/m/831868149f531f79808dbb4459aa4c39.png)