Greedy Nim

Nim, the classic combinatorial game where two players take turns choosing stones from piles, can be played with many variations. In the regular version, two players take turns removing any number of stones from a single pile in the game and the last player able to make a move wins. Greedy Nim is a variation where the players are restricted to choosing stones from only the largest pile.^[1]

Proof

Greedy Nim is a finite impartial game .

Let the largest number of stones in a pile be m, the second largest number of stones in a pile be n.

Let p_m be the number of piles having m stones, p_n be the number of piles having n stones.

Proposition: Game positions with p_m even are P positions ^[2]

Consider the positions where p_m is odd.

If p_m is larger than 1, we may remove all stones from this pile to reduce p_m by 1 and the new p_m will be even.

If p_m = 1 (i.e. the largest heap is unique), we have two cases:

• If p_n is odd, we reduce the size of the largest heap to n (so now the new p_m is even).

• If p_n is even, we remove the largest heap entirely, leaving an even number of largest heaps.

Thus we can move to a state where p_m is even.

Conversely, if p_m is even, if any move is possible (p_m ≠ 0) then it must take the game to a state where p_m is odd.

The final position of the game is even (p_m = 0). Hence each position of the game with p_m even must be a P position.

Greedy Nim Misère

Greedy Nim Misère has the same rules as Greedy Nim, but here the last player able to make a move loses

Analysis

The following is a list of some possible games and their positions (P = previous player win and N = Next player win with optimal game play), where 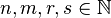and

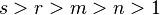
1 heap:

1 − P

n - N (reduce to 1)

2 heaps:

1,1 - N (reduce to 1)

1,n - N (reduce to 1)

n,n - P

n,m - N (reduce to n,n)

3 heaps:

1,1,1 - P

1,1,n - N (reduce to 1,1,1)

1,n,n - P

1,n,m - N (reduce to 1,n,n)

n,n,n - N (reduce to 1,n,n)

n,n,m - N (reduce to 1,n,n)

n,m,m - P

n,m,r - N (reduce to n,m,m)

4 heaps:

1,1,1,1 - N (reduce to 1,1,1)

1,1,1,n - N (reduce to 1,1,1)

1,1,n,n - P

1,1,n,m - N (reduce to 1,1,n,n)

1,n,m,m - P

1,n,m,r - N (reduce to 1,n,m,m)

n,n,n,n - P

n,n,n,m - N (reduce to n,n,n,n)

n,n,m,m - P

n,n,m,r - N (reduce to n,n,m,m)

n,m,m,m - N (reduce to n,n,m,m)

n,m,m,r - N (reduce to n,n,m,m)

n,m,r,r - P

n,m,r,s - N (reduce to n,m,r,r)

It can be observed that (with the exception of each heap only having one stone) an odd number of largest heaps will be an N game and an even number of largest piles will be a P game, just like in regular Greedy Nim. In the case that each heap only has one stone, the opposite is true – an even number of heaps is an N game and an odd number is a P game. Thus, whether you are playing Greedy Nim or its Misère version, optimal game play is the same until you get down to each heap having only one stone.

References