Great stellated truncated dodecahedron
| Great stellated truncated dodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 32, E = 90 V = 60 (χ = 2) |
| Faces by sides | 20{3}+12{10/3} |
| Wythoff symbol | 2 3 | 5/3 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U66, C83, W104 |
| Dual polyhedron | Great triakis icosahedron |
| Vertex figure |  3.10/3.10/3 |
| Bowers acronym | Quit Gissid |
In geometry, the great stellated truncated dodecahedron or quasitruncated great stellated dodecahedron is a nonconvex uniform polyhedron, indexed as U66. It is given a Schläfli symbol t0,1{5/3,3}.
Related polyhedra
It shares its vertex arrangement with three other uniform polyhedra: the small icosicosidodecahedron, the small ditrigonal dodecicosidodecahedron, and the small dodecicosahedron:
 Great stellated truncated dodecahedron |
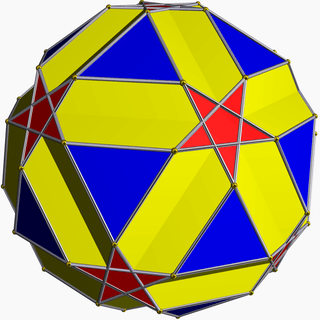 Small icosicosidodecahedron |
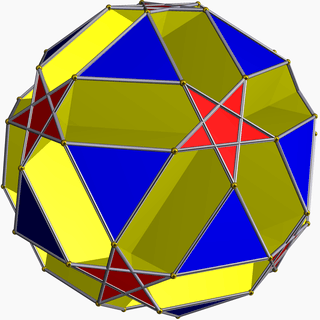 Small ditrigonal dodecicosidodecahedron |
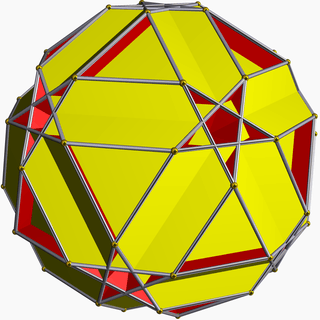 Small dodecicosahedron |
Cartesian coordinates
Cartesian coordinates for the vertices of a great stellated truncated dodecahedron are all the even permutations of
- (0, ±τ, ±(2−1/τ))
- (±τ, ±1/τ, ±2/τ)
- (±1/τ2, ±1/τ, ±2)
where τ = (1+√5)/2 is the golden ratio (sometimes written φ).