Great ellipse

For the shortest path between two points on the earth, see geodesics on an ellipsoid.

A great ellipse is an ellipse passing through two points on a spheroid and having the same center as that of the spheroid. Equivalently, it is an ellipse on the surface of spheroid and centered at the origin, or the curve formed by intersecting the spheroid by a plane through its center.^[1] For points which are separated by less than about a quarter of the circumference of the earth, about 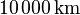$10\,000\,\mathrm{km}$ , the length of the great ellipse connecting the points is close (within one part in 500,000) to the geodesic distance.^[2]^[3]^[4] The great ellipse therefore is sometimes proposed as a suitable route for marine navigation.

Introduction

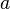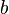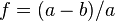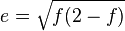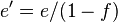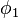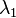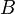Assume that the spheroid, an ellipsoid of revolution, has an equatorial radius $a$ and polar semi-axis $b$ . Define the flattening $f=(a-b)/a$ , the eccentricity $e=\sqrt{f(2-f)}$ , and the second eccentricity $e'=e/(1-f)$ . Consider two points: $A$ at (geographic) latitude $\phi_1$ and longitude $\lambda_1$ and $B$ at latitude 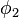$\phi_2$ and longitude 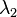$\lambda_2$ . 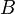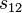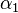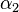The connecting great ellipse (from $A$ to $B$ ) has length $s_{12}$ and has azimuths $\alpha_1$ and $\alpha_2$ at the two endpoints.

There are various ways to map an ellipsoid into a sphere of radius 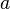$a$ in such a way as to map the great ellipse into a great circle, allowing the methods of great-circle navigation to be used:

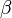The ellipsoid can be stretched in a direction parallel to the axis of rotation; this maps a point of latitude $\phi$ on the ellipsoid to a point on the sphere with latitude $\beta$ , the parametric latitude.
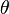A point on the ellipsoid can mapped radially onto the sphere along the line connecting it with the center of the ellipsoid; this maps a point of latitude $\phi$ on the ellipsoid to a point on the sphere with latitude $\theta$ , the geocentric latitude.
The ellipsoid can be stretched into a prolate ellipsoid with polar semi-axis 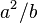$a^2/b$ and then mapped radially onto the sphere; this preserves the latitude—the latitude on the sphere is $\phi$ , the geographic latitude.

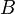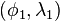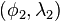The last method gives an easy way to generate a succession of way-points on the great ellipse connecting two known points $A$ and $B$ . Solve for the great circle between $(\phi_1,\lambda_1)$ and $(\phi_2,\lambda_2)$ and find the way-points on the great circle. These map into way-points on the corresponding great ellipse.

Mapping the great ellipse to a great circle

If distances and headings are needed, it is simplest to use the first of the mappings.^[5] In detail, the mapping is as follows (this description is taken from ^[6]):

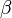The geographic latitude $\phi$ on the ellipsoid maps to the parametric latitude $\beta$ on the sphere, where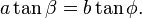
$a\tan\beta = b\tan\phi.$
The longitude 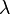$\lambda$ is unchanged.
The azimuth 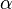$\alpha$ on the ellipsoid maps to an azimuth 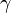$\gamma$ on the sphere where
$\begin{align} \tan\alpha &= \frac{\tan\gamma}{\sqrt{1-e^2\cos^2\beta}}, \\ \tan\gamma &= \frac{\tan\alpha}{\sqrt{1+e'^2\cos^2\phi}}, \end{align}$
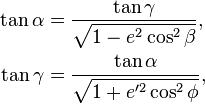
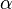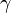and the quadrants of $\alpha$ and $\gamma$ are the same.
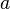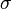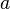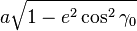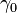Positions on the great circle of radius $a$ are parametrized by arc length $\sigma$ measured from the northward crossing of the equator. The great ellipse has a semi-axes $a$ and $a \sqrt{1 - e^2\cos^2\gamma_0}$ , where $\gamma_0$ is the great-circle azimuth at the northward equator crossing, and 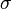$\sigma$ is the parametric angle on the ellipse.

(A similar mapping to an auxiliary sphere is carried out in the solution of geodesics on an ellipsoid. The differences are that the azimuth 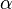$\alpha$ is conserved in the mapping, while the longtitude 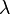$\lambda$ maps to a "spherical" longitude 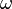$\omega$ . The equivalent ellipse used for distance calculations has semi-axes 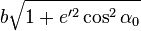$b \sqrt{1 + e'^2\cos^2\alpha_0}$ and $b$ .)

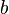Solving the inverse problem

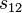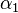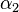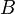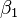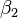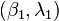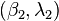The "inverse problem" is the determination of $s_{12}$ , $\alpha_1$ , and $\alpha_2$ , given the positions of $A$ and $B$ . This is solved by computing $\beta_1$ and $\beta_2$ and solving for the great-circle between $(\beta_1,\lambda_1)$ and $(\beta_2,\lambda_2)$ .

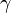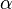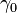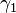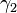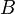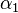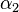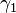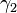The spherical azimuths are relabeled as $\gamma$ (from $\alpha$ ). Thus $\gamma_0$ , $\gamma_1$ , and $\gamma_2$ and the spherical azimuths at the equator and at $A$ and $B$ . The azimuths of the endpoints of great ellipse, $\alpha_1$ and $\alpha_2$ , are computed from $\gamma_1$ and $\gamma_2$ .

The semi-axes of the great ellipse can be found using the value of 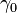$\gamma_0$ .

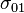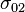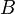Also determined as part of the solution of the great circle problem are the arc lengths, $\sigma_{01}$ and $\sigma_{02}$ , measured from the equator crossing to $A$ and $B$ . The distance 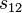$s_{12}$ is found by computing the length of a portion of perimeter of the ellipse using the formula giving the meridian arc in terms the parametric latitude. 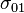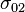In applying this formula, use the semi-axes for the great ellipse (instead of for the meridian) and substitute $\sigma_{01}$ and $\sigma_{02}$ for $\beta$ .

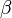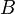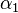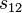The solution of the "direct problem", determining the position of $B$ given $A$ , $\alpha_1$ , and $s_{12}$ , can be similarly be found (this requires, in addition, the inverse meridian distance formula). This also enables way-points (e.g., a series of equally spaced intermediate points) to be found in the solution of the inverse problem.

References

↑ American Society of Civil Engineers (1994), Glossary of Mapping Science, ASCE Publications, p. 172, ISBN 9780784475706 .
↑ Bowring, B. R. (1984). "The direct and inverse solutions for the great elliptic line on the reference ellipsoid". Bulletin Géodésique 58: 101–108. doi:10.1007/BF02521760.
↑ Williams, R. (1996). "The Great Ellipse on the Surface of the Spheroid". Journal of Navigation 49 (2): 229–234. doi:10.1017/S0373463300013333.
↑ Walwyn, P. R. (1999). "The Great Ellipse Solution for Distances and Headings to Steer between Waypoints". Journal of Navigation 52 (3): 421–424. doi:10.1017/S0373463399008516.
↑ Sjöberg, L. E. (2012c). "Solutions to the direct and inverse navigation problems on the great ellipse". Journal of Geodetic Science 2 (3): 200–205. doi:10.2478/v10156-011-0040-9.
↑ Karney, C. F. F. (2014). "Great ellipses". From the documentation of GeographicLib 1.38.

External links