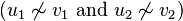Graph product
In mathematics, a graph product is a binary operation on graphs. Specifically, it is an operation that takes two graphs G1 and G2 and produces a graph H with the following properties:
- The vertex set of H is the Cartesian product V(G1) × V(G2), where V(G1) and V(G2) are the vertex sets of G1 and G2, respectively.
- Two vertices (u1, u2) and (v1, v2) of H are connected by an edge if and only if the vertices u1, u2, v1, v2 satisfy conditions of a certain type (see below).
The following table shows the most common graph products, with ∼ denoting “is connected by an edge to”, and 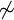 denoting non-connection. The operator symbols listed here are by no means standard, especially in older papers.
denoting non-connection. The operator symbols listed here are by no means standard, especially in older papers.
| Name | Condition for (u1, u2) ∼ (v1, v2). | Dimensions | Example |
|---|---|---|---|
Cartesian product |
( u1 = v1 and u2 ∼ v2 ) or ( u1 ∼ v1 and u2 = v2 ) |
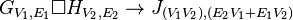 |
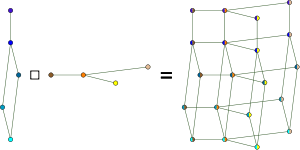 |
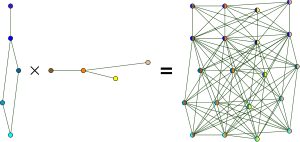
| Tensor product (Categorical product) 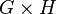 |
u1 ∼ v1 and u2 ∼ v2 | 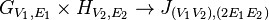 |
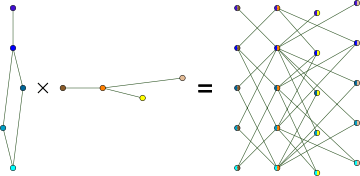 |
Lexicographical product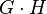 or or ![G[H]](../I/m/6904db9590e056b9affcf0b4c3011664.png) |
u1 ∼ v1 or ( u1 = v1 and u2 ∼ v2 ) |
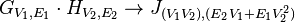 |
 |
| Strong product (Normal product, AND product) 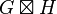 |
( u1 = v1 and u2 ∼ v2 ) or ( u1 ∼ v1 and u2 = v2 ) or ( u1 ∼ v1 and u2 ∼ v2 ) |
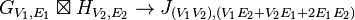 |
|
| Co-normal product (disjunctive product, OR product) 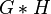 |
u1 ∼ v1 or u2 ∼ v2 |
||
| Modular product | 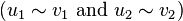 or
|
||
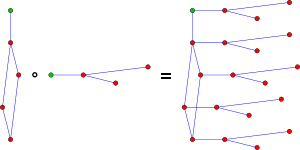
| Rooted product | see article |  |
 |
| Kronecker product | see article | see article | see article |
| Zig-zag product | see article | see article | see article |
| Replacement product | |||
Homomorphic product[1][2]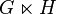 |
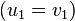 or 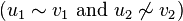 |
In general, a graph product is determined by any condition for (u1, u2) ∼ (v1, v2) that can be expressed in terms of the statements u1 ∼ v1, u2 ∼ v2, u1 = v1, and u2 = v2.
Mnemonic
Let  be the complete graph on two vertices (i.e. a single edge). The product graphs
be the complete graph on two vertices (i.e. a single edge). The product graphs  ,
, 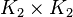 , and
, and 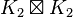 look exactly like the glyph representing the operator. For example,
look exactly like the glyph representing the operator. For example,  is a four cycle (a square) and
is a four cycle (a square) and 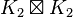 is the complete graph on four vertices. The
is the complete graph on four vertices. The ![G[H]](../I/m/6904db9590e056b9affcf0b4c3011664.png) notation for lexicographic product serves as a reminder that this product is not commutative.
notation for lexicographic product serves as a reminder that this product is not commutative.
See also
Notes
- ↑ 1.0 1.1 Roberson, David E.; Mancinska, Laura (2012). "Graph Homomorphisms for Quantum Players". arXiv:1212.1724 [quant-ph].
- ↑ The hom-product of [3] is the graph complement of the homomorphic product of.[1]
- ↑ Bačík, R.; Mahajan, S. (1995). "Semidefinite programming and its applications to NP problems". Computing and Combinatorics. Lecture Notes in Computer Science 959. p. 566. doi:10.1007/BFb0030878. ISBN 3-540-60216-X.
References
- Imrich, Wilfried; Klavžar, Sandi (2000). Product Graphs: Structure and Recognition. Wiley. ISBN 0-471-37039-8{{inconsistent citations}}.