Graph coloring game
The graph coloring game is a mathematical game related to graph theory. Coloring game problems arose as game-theoretic versions of well-known graph coloring problems. In a coloring game, two players are using a given set of colors to construct a coloring of a graph, following specific rules depending on the game we consider. One player tries to completes successfully the coloring of the graph, when the other one tries to prevent him to achieve it.
Vertex coloring game
The vertex coloring game was introduced in 1981 by Brahms[1] and rediscovered ten years after by Bodlaender.[2] Its rules are as follows:
- Alice and Bob are coloring the vertices of a graph G with a set k of colors.
- Alice and Bob are taking turns, coloring properly a uncolored vertex (in the standard version, Alice begins).
- If a vertex v is impossible to color properly (for any color, v has a neighbor colored with it), then Bob wins.
- If the graph is completely colored, then Alice wins.
The game chromatic number of a graph  , denoted by
, denoted by 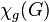 , is the minimum number of colors needed for Alice to win the vertex coloring game on
, is the minimum number of colors needed for Alice to win the vertex coloring game on  . Trivially, for every graph
. Trivially, for every graph  , we have
, we have 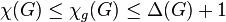 , where
, where 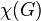 is the chromatic number of
is the chromatic number of  and
and 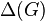 its maximum degree.[3]
its maximum degree.[3]
Relation with other notions
Acyclic coloring. Every graph  with acyclic chromatic number
with acyclic chromatic number  has
has 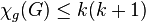 .[4]
.[4]
Marking game. For every graph  ,
, 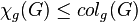 , where
, where 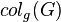 is the game coloring number of
is the game coloring number of  . Almost every known upper bound for the game chromatic number of graphs are obtained from bounds on the game coloring number.
. Almost every known upper bound for the game chromatic number of graphs are obtained from bounds on the game coloring number.
Cycle-restrictions on edges. If every edge of a graph  belongs to at most
belongs to at most  cycles, then
cycles, then 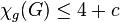 .[5]
.[5]
Graph Classes
For a class 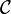 of graphs, we denote by
of graphs, we denote by 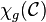 the smallest integer
the smallest integer  such that every graph
such that every graph  of
of 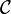 has
has 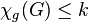 . In other words,
. In other words, 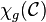 is the exact upper bound for the game chromatic number of graphs in this class. This value is known for several standard graph classes, and bounded for some others:
is the exact upper bound for the game chromatic number of graphs in this class. This value is known for several standard graph classes, and bounded for some others:
- Forests:
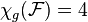 .[6] Simple criteria are known to determine the game chromatic number of a forest without vertex of degree 3.[7] It seems difficult to determine the game chromatic number of forests with vertices of degree 3, even for forests with maximum degree 3.
.[6] Simple criteria are known to determine the game chromatic number of a forest without vertex of degree 3.[7] It seems difficult to determine the game chromatic number of forests with vertices of degree 3, even for forests with maximum degree 3. - Cactuses:
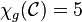 .[8]
.[8] - Outerplanar graphs:
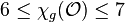 .[9]
.[9] - Planar graphs:
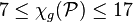 .[10]
.[10] - Planar graphs of given girth:
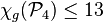 ,[11]
,[11] 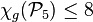 ,
, 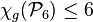 ,
, 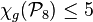 .[12]
.[12] - Toroidal grids:
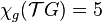 .[13]
.[13] - Partial k-trees:
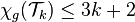 .[14]
.[14] - Interval graphs:
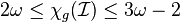 , where
, where 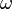 is for a graph the size of its largest clique.[15]
is for a graph the size of its largest clique.[15]
Cartesian products.
The game chromatic number of the cartesian product  is not bounded by a function of
is not bounded by a function of 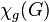 and
and 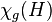 . In particular, the game chromatic number of any complete bipartite graph
. In particular, the game chromatic number of any complete bipartite graph 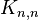 is equal to 3, but there is no upper bound for
is equal to 3, but there is no upper bound for 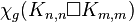 for arbitrary
for arbitrary 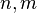 .[16]
.[16]
-
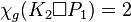 ,
,
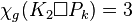 if
if 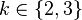 ,
,
and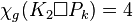 if
if 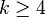 .[16]
.[16] - For any
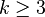 ,
, 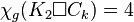 .[16]
.[16] - For any
 ,
, 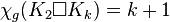 .[16]
.[16] - Trees :
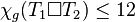 .
. - Stars :
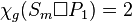 ,
, 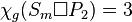 ,
,
and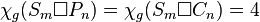 if
if 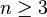 .[17]
.[17] - Wheels :
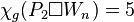 if
if 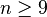 .[17]
.[17] - Complete bipartite graphs :
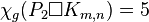 if
if 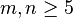 .[17]
.[17]
Open problems
These questions are still open to this date.
- Suppose Alice has a winning strategy for the vertex coloring game on a graph G with k colors. Does she have one for k+1 colors ?
One would expect the answers to be "yes", as having more colors seems an advantage to Alice. However, no proof exists that this statement is true. - Is there a function f such that, if Alice has a winning strategy for the vertex coloring game on a graph G with k colors, then Alice has a winning strategy on G with f(k) ?
Relaxation of the previous question.
- Suppose a hereditary class of graphs (i.e. a class of graphs closed by subgraphs) has bounded game chromatic number. Is it true that this class of graph has bounded game coloring number ?
- Suppose a hereditary class of graphs (i.e. a class of graphs closed by subgraphs) has bounded game chromatic number. Is it true that this class of graph has bounded arboricity ?
- Is it true that a hereditary class of graphs of bounded game chromatic number has bounded acyclic chromatic number ?
- Conjecture: Is
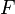 is a forest, there exists
is a forest, there exists 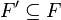 such that
such that 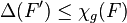 and
and 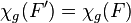 .
. - Let
 be the class of graphs such that for any
be the class of graphs such that for any 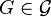 , there exists
, there exists 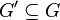 such that
such that 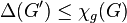 and
and 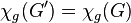 . What families of graphs are in
. What families of graphs are in  ?
?
Edge coloring game
The edge coloring game, introduced by Lam, Shiu and Zu,[19] is similar to the vertex coloring game, except Alice and Bob construct a proper edge coloring instead of a proper vertex coloring. Its rules are as follows:
- Alice and Bob are coloring the edges a graph G with a set k of colors.
- Alice and Bob are taking turns, coloring properly a uncolored edge (in the standard version, Alice begins).
- If an edge e is impossible to color properly (for any color, e is adjacent to an edge colored with it), then Bob wins.
- If the graph is completely edge-colored, then Alice wins.
Although this game can be considered as a particular case of the vertex coloring game on line graphs, it is mainly considered in the scientific literature as a distinct game. The game chromatic index of a graph  , denoted by
, denoted by 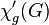 , is the minimum number of colors needed for Alice to win this game on
, is the minimum number of colors needed for Alice to win this game on  .
.
General case
For every graph G, 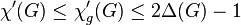 . There are graphs reaching these bounds but all the graphs we know reaching this upper bound have small maximum degree.[19]
There exists graphs with
. There are graphs reaching these bounds but all the graphs we know reaching this upper bound have small maximum degree.[19]
There exists graphs with 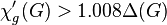 for arbitrary large values of
for arbitrary large values of 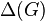 .[20]
.[20]
Conjecture. There is an 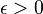 such that, for any arbitrary graph
such that, for any arbitrary graph  , we have
, we have 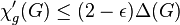 .
.
This conjecture is true when 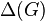 is large enough compared to the number of vertices in
is large enough compared to the number of vertices in  .[20]
.[20]
- Arboricity. Let
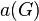 be the arboricity of a graph
be the arboricity of a graph  . Every graph
. Every graph  with maximum degree
with maximum degree 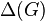 has
has 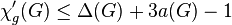 .[21]
.[21]
Graph Classes
For a class 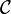 of graphs, we denote by
of graphs, we denote by 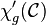 the smallest integer
the smallest integer  such that every graph
such that every graph  of
of 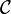 has
has 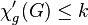 . In other words,
. In other words, 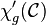 is the exact upper bound for the game chromatic index of graphs in this class. This value is known for several standard graph classes, and bounded for some others:
is the exact upper bound for the game chromatic index of graphs in this class. This value is known for several standard graph classes, and bounded for some others:
- Wheels:
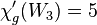 and
and 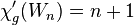 when
when 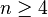 .[19]
.[19] - Forests :
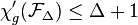 when
when 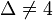 , and
, and 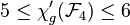 .[22]
.[22]
Moreover, if every tree of a forest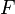 of
of 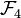 is obtained by subdivision from a caterpillar tree or contains no two adjacent vertices with degree 4, then
is obtained by subdivision from a caterpillar tree or contains no two adjacent vertices with degree 4, then 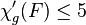 .[23]
.[23]
Open Problems
Upper bound. Is there a constant 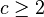 such that
such that 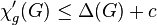 for each graph
for each graph  ? If it is true, is
? If it is true, is 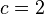 enough ?[19]
enough ?[19]
Conjecture on large minimum degrees. There are a 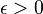 and an integer
and an integer 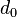 such that any graph
such that any graph  with
with 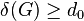 satisfies
satisfies 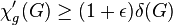 . [20]
. [20]
Incidence coloring game
The incidence coloring game is a graph coloring game, introduced by Andres,[24] and similar to the vertex coloring game, except Alice and Bob construct a proper incidence coloring instead of a proper vertex coloring. Its rules are as follows:
- Alice and Bob are coloring the incidences of a graph G with a set k of colors.
- Alice and Bob are taking turns, coloring properly a uncolored incidence (in the standard version, Alice begins).
- If an incidence i is impossible to color properly (for any color, i is adjacent to an incident colored with it), then Bob wins.
- If all the incidences are properly colored, then Alice wins.
The incidence game chromatic number of a graph  , denoted by
, denoted by 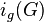 , is the minimum number of colors needed for Alice to win this game on
, is the minimum number of colors needed for Alice to win this game on  .
.
For every graph  with maximum degree
with maximum degree 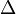 , we have
, we have 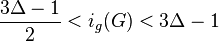 .[24]
.[24]
Relations with other notions
- (a,d)-Decomposition. This is the best upper bound we know for the general case. If the edges of a graph
 can be partitionned into two sets, one of them inducing a graph with arboricity
can be partitionned into two sets, one of them inducing a graph with arboricity  , the second inducing a graph with maximum degree
, the second inducing a graph with maximum degree  , then
, then 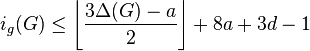 .[25]
.[25]
If moreover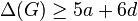 , then
, then 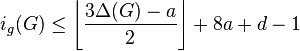 .[25]
.[25]
- Degeneracy. If
 is a k-degenerated graph with maximum degree
is a k-degenerated graph with maximum degree 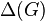 , then
, then 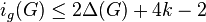 . Moreover,
. Moreover, 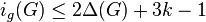 when
when 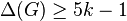 and
and 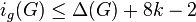 when
when 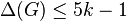 .[24]
.[24]
Graph Classes
For a class 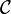 of graphs, we denote by
of graphs, we denote by 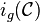 the smallest integer
the smallest integer  such that every graph
such that every graph  of
of 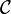 has
has 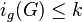 .
.
- Paths : For
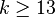 ,
, 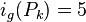 .
. - Cycles : For
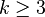 ,
, 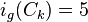 .[26]
.[26] - Stars : For
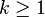 ,
, 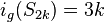 .[24]
.[24] - Wheels : For
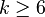 ,
, 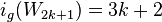 . For
. For 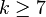 ,
, 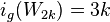 .[24]
.[24] - Subgraphs of Wheels : For
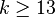 , if
, if  is a subgraph of
is a subgraph of 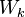 having
having 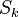 as a subgraph, then
as a subgraph, then 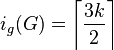 .[27]
.[27]
Open Problems
- Is the upper bound
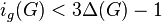 tight for every value of
tight for every value of 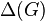 ?[24]
?[24] - Is the incidence game chromatic number a monotonic parameter (i.e. is it as least as big for a graph G as for any subgraph of G) ?[24]
Notes
- ↑ Gardner (1981)
- ↑ Bodlaender (1991)
- ↑ With less colors than the chromatic number, there is no proper coloring of G and so Alice cannot win. With most colors than the maximum degree, there is always an available color for coloring a vertex and so Alice cannot lose.
- ↑ Dinski & Zhu (1999)
- ↑ Junosza-Szaniawski & Roej (2010)
- ↑ Faigle et al. (1993), and implied by Junosza-Szaniawski & Roej (2010)
- ↑ 7.0 7.1 Dunn et al. (2014)
- ↑ Sidorowicz (2007), and implied by Junosza-Szaniawski & Roej (2010)
- ↑ Guan & Zhu (1999)
- ↑ Upper bound by Zhu (2008), improving previous bounds of 33 in Kierstead & Trotter (1994), 30 implied by Dinski & Zhu (1999), 19 in Zhu (1999) and 18 in Kierstead (2000). Lower bound claimed by Kierstead & Trotter (1994). See a survey dedicated to the game chromatic number of planar graphs in Bartnicki et al. (2007).
- ↑ Sekigushi (2014)
- ↑ He et al. (2002)
- ↑ Raspaud & Wu (2009)
- ↑ Zhu (2000)
- ↑ Faigle et al. (1993)
- ↑ 16.0 16.1 16.2 16.3 16.4 16.5 Peterin (2007)
- ↑ 17.0 17.1 17.2 Sia (2009)
- ↑ 18.0 18.1 Zhu (1999)
- ↑ 19.0 19.1 19.2 19.3 Lam, Shiu & Zu (1999)
- ↑ 20.0 20.1 20.2 Beveridge et al. (2008)
- ↑ Bartnicki & Grytczuk (2008), improving results on k-degenerated graphs in Cai & Zhu (2001)
- ↑ Upper bound of Δ+2 by Lam, Shiu & Zu (1999), then bound of Δ+1 by Erdös et al. (2004) for cases Δ=3 and Δ≥6, and by Andres (2006) for case Δ=5.
- ↑ Conditions on forests with Δ=4 are in Chan & Nong (2014)
- ↑ 24.0 24.1 24.2 24.3 24.4 24.5 24.6 Andres (2009a), see also erratum in Andres (2009b)
- ↑ 25.0 25.1 Charpentier & Sopena (2014), extending results of Charpentier & Sopena (2013).
- ↑ Kim (2011), improving a similar result for k ≥ 7 in Andres (2009a) (see also erratum in Andres (2009b))
- ↑ Kim (2011)
References (chronological order)
- Gardner, Martin (1981). "Mathematical Games". Scientific American 23.
- Bodlaender, Hans L. (1991). "On the complexity of some coloring games". Lecture Notes in Computer Science 484: pp. 30–40. doi:10.1007/3-540-53832-1_29.
- Faigle, Ulrich; Kern, Walter; Kierstead, Henry A.; Trotter, William T. (1993). "On the Game Chromatic Number of some Classes of Graphs". Ars Combinatoria 35 (17): pp. 143–150.
- Kierstead, Henry A.; Trotter, William T. (1994). "Planar Graph Coloring with an Uncooperative Partner". Journal of Graph Theory 18 (6): pp. 564–584. doi:10.1002/jgt.3190180605.
- Dinski, Thomas; Zhu, Xuding (1999). "A bound for the game chromatic number of graphs". Discrete Mathematics 196: pp. 109–115. doi:10.1016/s0012-365x(98)00197-6.
- Guan, D. J.; Zhu, Xuding (1999). "Game chromatic number of outerplanar graphs". Journal of Graph Theory 30 (1): pp. 67–70. doi:10.1002/(sici)1097-0118(199901)30:1<67::aid-jgt7>3.0.co;2-m.
- Lam, Peter C. B.; Shiu, Wai C.; Xu, Baogang (1999). "Edge game coloring of graphs". Graph Theory Notes N.Y. 37: pp. 17–19.
- Zhu, Xuding (1999). "The Game Coloring Number of Planar Graphs". Journal of Combinatorial Theory, Series B 75 (2): pp. 245–258. doi:10.1006/jctb.1998.1878.
- Kierstead, Henry A. (2000). "A Simple Competitive Graph Coloring Algorithm". Journal of Combinatorial Theory, Series B 78 (1): pp. 57–68. doi:10.1006/jctb.1999.1927.
- Zhu, Xuding (2000). "The game coloring number of pseudo partial k-trees". Discrete Mathematics 215 (1-3): pp. 245–262. doi:10.1016/s0012-365x(99)00237-x.
- Cai, Leizhen; Zhu, Xuding (2001). "Game Chromatic Index of k-Degenerate Graphs". Journal of Graph Theory 36: pp. 144–155. doi:10.1002/1097-0118(200103)36:3<144::aid-jgt1002>3.0.co;2-f.
- He, Wenjie; Hou, Xiaoling; Lih, Ko-Wei; Shao, Jiating; Wang, Weifan; Zhu, Xuding (2002). "Edge-partitions of planar graphs and their game coloring numbers". Journal of Graph Theory 41: pp. 307–311. doi:10.1002/jgt.10069.
- Erdös, Peter L.; Faigle, Ulrich; Hochstättler, Winfried; Kern, Walter (2004). "Note on the game chromatic index of trees". Theoretical Computer Science 313 (3): pp. 371–376. doi:10.1016/j.tcs.2002.10.002.
- Andres, Stephan D. (2006). "The game chromatic index of forests of maximum degree Δ ⩾ 5". Discrete Applied Mathematics 154 (9): pp. 1317–1323. doi:10.1016/j.dam.2005.05.031.
- Bartnicki, Tomasz; Grytczuk, Jaroslaw; Kierstead, H. A.; Xuding (2007). "The Map-Coloring Game". American Mathematical Monthly 114 (9): pp. 793–803.
- Peterin, Iztok (2007). "Game chromatic number of Cartesian product graphs". Electronic Notes in Discrete Mathematics 29: pp. 353–357. doi:10.1016/j.endm.2007.07.060.
- Sidorowicz, Elżbieta (2007). "The game chromatic number and the game colouring number of cactuses". Information Processing Letters 102: pp. 147–151. doi:10.1016/j.ipl.2006.12.003.
- Bartnicki, Tomasz; Grytczuk, Jarosław (2008). "A Note on the Game Chromatic Index of Graphs". Graphs and Combinatorics 24 (2): pp. 67–70. doi:10.1007/s00373-008-0774-z.
- Beveridge, Andrew; Bohman, Tom; Friezeb, Alan; Pikhurko, Oleg (2008). "Game chromatic index of graphs with given restrictions on degrees". Theoretical Computer Science 407 (1-3): pp. 242–249. doi:10.1016/j.tcs.2008.05.026.
- Zhu, Xuding (2008). "Refined activation strategy for the marking game". Journal of Combinatorial Theory, Series B 98 (1): pp. 1–18. doi:10.1016/j.jctb.2007.04.004.
- Andres, Stefan D. (2009). "The incidence game chromatic number". Discrete Applied Mathematics 157 (9): pp. 1980–1987. doi:10.1016/j.dam.2007.10.021.
- Andres, Stefan D. (2009). "Erratum to: The incidence game chromatic number". Discrete Applied Mathematics 158 (6): p. 728. doi:10.1016/j.dam.2009.11.017.
- Raspaud, André; Jiaojiao, Wu (2009). "Game chromatic number of toroidal grids". Information Processing Letters 109 (21-22): pp. 1183–1186. doi:10.1016/j.ipl.2009.08.001.
- Sia, Charmaine (2009). "The Game Chromatic Number of Some Families of Cartesian Product Graphs". AKCE International Journal of Graphs and Combinatorics 6 (2): pp. 315–327.
- Junosza-Szaniawski, Konstanty; Roej, Łukasz (2010). "Game chromatic number of graphs with locally bounded number of cycles". Information Processing Letters 110 (17): pp. 757–760. doi:10.1016/j.ipl.2010.06.004.
- Kim, John Y. (2011). "The incidence game chromatic number of paths and subgraphs of wheels". Discrete Applied Mathematics 159 (8): pp. 683–694. doi:10.1016/j.dam.2010.01.001.
- Charpentier, Clément; Sopena, Éric (2013). "Incidence coloring game and arboricity of graphs". Lecture Notes in Computer Science 8288: pp. 106–114. doi:10.1007/978-3-642-45278-9_10.
- Chan, Wai H.; Nong, Ge (2014). "The game chromatic index of some trees of maximum degree 4". Discrete Applied Mathematics 170: pp. 1–6. doi:10.1016/j.dam.2014.01.003.
- Sekigushi, Yosuke (2014). "The game coloring number of planar graphs with a given girth". Discrete Mathematics 300: pp. 11–16. doi:10.1016/j.disc.2014.04.011.
- Charpentier, Clément; Sopena, Éric (2014). "The incidence game chromatic number of (a,d)-decomposable graphs". Journal of Discrete Algorithms. doi:10.1016/j.jda.2014.10.001.
- Dunn, Charles; Larsen, Victor; Lindke, Kira; Retter, Troy; Toci, Ducin (2014). "The game chromatic number of trees and forests". ArXiV deposit.
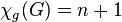 for any hypercube
for any hypercube 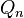 ?
? 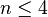 .
.