Graded manifold

In algebraic geometry, Graded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Both graded manifolds and supermanifolds are phrased in terms of sheaves of graded commutative algebras. However, graded manifolds are characterized by sheaves on smooth manifolds, while supermanifolds are constructed by gluing of sheaves of supervector spaces.

Graded manifolds

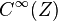A graded manifold of dimension $(n,m)$ is defined as a locally ringed space $(Z,A)$ where $Z$ is an $n$ -dimensional smooth manifold and $A$ is a $C^\infty_Z$ -sheaf of Grassmann algebras of rank $m$ where $C^\infty_Z$ is the sheaf of smooth real functions on $Z$ . A sheaf $A$ is called the structure sheaf of a graded manifold $(Z,A)$ , and a manifold $Z$ is said to be the body of $(Z,A)$ . Sections of the sheaf $A$ are called graded functions on a graded manifold $(Z,A)$ . 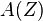They make up a graded commutative $C^\infty(Z)$ -ring $A(Z)$ called the structure ring of $(Z,A)$ . The well-known Batchelor theorem and Serre-Swan theorem characterize graded manifolds as follows.

Serre-Swan theorem for graded manifolds

Let $(Z,A)$ be a graded manifold. There exists a vector bundle $E\to Z$ with an $m$ -dimensional typical fiber $V$ such that the structure sheaf $A$ of $(Z,A)$ is isomorphic to the structure sheaf of sections of the exterior product $\Lambda(E)$ of $E$ , whose typical fibre is the Grassmann algebra 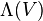$\Lambda(V)$ .

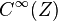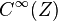Let $Z$ be a smooth manifold. A graded commutative $C^\infty(Z)$ -algebra is isomorphic to the structure ring of a graded manifold with a body $Z$ if and only if it is the exterior algebra of some projective $C^\infty(Z)$ -module of finite rank.

Graded functions

Note that above mentioned Batchelor's isomorphism fails to be canonical, but it often is fixed from the beginning. In this case, every trivialization chart 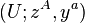$(U; z^A,y^a)$ of the vector bundle $E\to Z$ yields a splitting domain $(U; z^A,c^a)$ of a graded manifold $(Z,A)$ , where $\{c^a\}$ is the fiber basis for $E$ . Graded functions on such a chart are 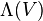$\Lambda(V)$ -valued functions

$f=\sum_{k=0}^m \frac1{k!}f_{a_1\ldots a_k}(z)c^{a_1}\cdots c^{a_k}$ ,

where $f_{a_1\cdots a_k}(z)$ are smooth real functions on $U$ and $c^a$ are odd generating elements of the Grassmann algebra 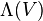$\Lambda(V)$ .

Graded vector fields

Given a graded manifold $(Z,A)$ , graded derivations of the structure ring of graded functions 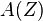$A(Z)$ are called graded vector fields on $(Z,A)$ . They constitute a real Lie superalgebra $\partial A(Z)$ with respect to the superbracket

$[u,u']=u\cdot u'-(-1)^{[u][u']}u'\cdot u$ ,

where $[u]$ denotes the Grassmann parity of $u\in \partial A(Z)$ . Graded vector fields locally read

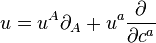$u= u^A\partial_A + u^a\frac{\partial}{\partial c^a}$ .

They act on graded functions $f$ by the rule

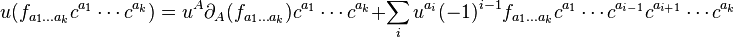$u(f_{a_1\ldots a_k}c^{a_1}\cdots c^{a_k})=u^A\partial_A(f_{a_1\ldots a_k})c^{a_1}\cdots c^{a_k}+ \sum_i u^{a_i}(-1)^{i-1} f_{a_1\ldots a_k}c^{a_1}\cdots c^{a_{i-1}}c^{a_{i+1}}\cdots c^{a_k}$ .

Graded exterior forms

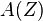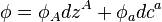The $A(Z)$ -dual of the module graded vector fields $\partial A(Z)$ is called the module of graded exterior one-forms $O^1(Z)$ . Graded exterior one-forms locally read $\phi=\phi_A dz^A + \phi_adc^a$ so that the duality (interior) product between $\partial A(Z)$ and $O^1(Z)$ takes the form

$u\rfloor \phi=u^A\phi_A + (-1)^{[\phi_a]}u^a\phi_a$ .

Provided with the graded exterior product

$dz^A\wedge dc^i=-dc^i\wedge dz^A, \qquad dc^i\wedge dc^j= dc^j\wedge dc^i$ ,

graded one-forms generate the graded exterior algebra 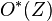$O^*(Z)$ of graded exterior forms on a graded manifold. They obey the relation

$\phi\wedge\phi'=(-1)^{|\phi||\phi'| +[\phi][\phi']}\phi'\wedge\phi$ ,

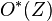where $|\phi|$ denotes the form degree of $\phi$ . The graded exterior algebra $O^*(Z)$ is a graded differential algebra with respect to the graded exterior differential

$d\phi= dz^A \wedge \partial_A\phi +dc^a\wedge \frac{\partial}{\partial c^a}\phi$ ,

where the graded derivations 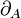$\partial_A$ , $\partial/\partial c^a$ are graded commutative with the graded forms $dz^A$ and $dc^a$ . There are the familiar relations

$d(\phi\wedge\phi')=d(\phi)\wedge\phi' +(-1)^{|\phi|}\phi\wedge d\phi'$ .

Graded differential geometry

In the category of graded manifolds, one considers graded Lie groups, graded bundles and graded principal bundles. One also introduces the notion of jets of graded manifolds, but they differ from jets of graded bundles.

Graded differential calculus

The differential calculus on graded manifolds is formulated as the differential calculus over graded commutative algebras similarly to the differential calculus over commutative algebras.

Physical outcome

Due to the above-mentioned Serre-Swan theorem, odd classical fields on a smooth manifold are described in terms of graded manifolds. Extended to graded manifolds, the variational bicomplex provides the strict mathematical formulation of Lagrangian classical field theory and Lagrangian BRST theory.

References

C. Bartocci, U. Bruzzo, D. Hernandez Ruiperez, The Geometry of Supermanifolds (Kluwer, 1991) ISBN 0-7923-1440-9
T. Stavracou, Theory of connections on graded principal bundles, Rev. Math. Phys. 10 (1998) 47
B. Kostant, Graded manifolds, graded Lie theory, and prequantization, in Differential Geometric Methods in Mathematical Physics, Lecture Notes in Mathematics 570 (Springer, 1977) p. 177
A. Almorox, Supergauge theories in graded manifolds, in Differential Geometric Methods in Mathematical Physics, Lecture Notes in Mathematics 1251 (Springer, 1987) p. 114
D. Hernandez Ruiperez, J. Munoz Masque, Global variational calculus on graded manifolds, J. Math. Pures Appl. 63 (1984) 283
G. Giachetta, L. Mangiarotti, G. Sardanashvily, Advanced Classical Field Theory (World Scientific, 2009) ISBN 978-981-283-895-7; arXiv: math-ph/0102016; arXiv: 1304.1371.

External links

G. Sardanashvily, Lectures on supergeometry, arXiv: 0910.0092.