Graded category

A graded category is a mathematical concept.

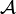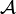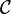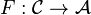If $\mathcal{A}$ is a category, then a $\mathcal{A}$ -graded category is a category $\mathcal{C}$ together with a functor $F:\mathcal{C} \rightarrow \mathcal{A}$ .

Monoids and groups can be thought of as categories with a single element. A monoid-graded or group-graded category is therefore one in which to each morphism is attached an element of a given monoid (resp. group), its grade. This must be compatible with composition, in the sense that compositions have the product grade.

Definition

There are various different definitions of a graded category, up to the most abstract one given above. A more concrete definition of a semigroup-graded Abelian category is as follows:^[1]

Let 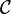$\mathcal{C}$ be an Abelian category and 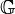$\mathbb{G}$ a semigroup. Let 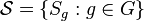$\mathcal{S}=\{ S_{g} : g\in G \}$ be a set of functors from 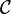$\mathcal{C}$ to itself. If

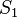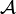$S_{1}$ is the identity functor on $\mathcal{A}$ ,
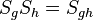$S_{g}S_{h}=S_{gh}$ for all 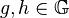$g,h\in \mathbb{G}$ and
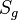$S_{g}$ is a full and faithful functor for every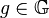 $g\in \mathbb{G}$

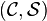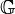we say that $(\mathcal{C},\mathcal{S})$ is a $\mathbb{G}$ -graded category.

References

↑ Zhang, J. J. (1 March 1996). "Twisted Graded Algebras and Equivalences of Graded Categories". Proceedings of the London Mathematical Society. s3-72 (2): 281–311. doi:10.1112/plms/s3-72.2.281.

Graded category

Definition

See also

References