Gowers norm

"Uniformity norm" redirects here. For the function field norm, see uniform norm. For unformity in topology, see uniform space.

In mathematics, in the field of additive combinatorics, a Gowers norm or uniformity norm is a class of norm on functions on a finite group or group-like object which are used in the study of arithmetic progressions in the group. It is named after Timothy Gowers, who introduced it in his work on Szemerédi's theorem.

Let f be a complex-valued function on a finite Abelian group G and let J denote complex conjugation. The Gowers d-norm is

\Vert f \Vert_{U^d(G)}^{2^d} = \mathbf{E}_{x,h_1,\ldots,h_d \in G} \prod_{\omega_1,\ldots,\omega_d \in \{0,1\}} J^{\omega_1+\cdots+\omega_d} f\left({x + h_1\omega_1 + \cdots + h_d\omega_d}\right) \ .

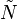Gowers norms are also defined for complex valued functions f on a segment [N]={0,1,2,...,N-1}, where N is a positive integer. 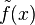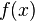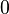In this context, the uniformity norm is given as $\Vert f \Vert_{U^d[N]} = \Vert \tilde{f} \Vert_{U^d(\mathbb{Z}/\tilde{N}\mathbb{Z})}/\Vert 1_{[N]} \Vert_{U^d(\mathbb{Z}/\tilde{N}\mathbb{Z})}$ , where $\tilde N$ is a large integer, $1_{[N]}$ denotes the indicator function of [N], and $\tilde f(x)$ is equal to $f(x)$ for $x \in [N]$ and $0$ for all other 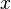$x$ . 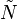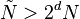This definition does not depend on $\tilde N$ , as long as $\tilde N > 2^d N$ .

An inverse conjecture for these norms is a statement asserting that if a bounded function f has a large Gowers d-norm then f correlates with a polynomial phase of degree d-1 or other object with polynomial behaviour (e.g. a (d-1)-step nilsequence). The precise statement depends on the Gowers norm under consideration.

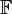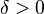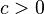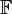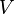The Inverse Conjecture for vector spaces over a finite field $\mathbb F$ asserts that for any $\delta > 0$ there exists a constant $c > 0$ such that for any finite dimensional vector space V over $\mathbb F$ and any complex valued function $f$ on $V$ , bounded by 1, such that $\Vert f \Vert_{U^{d}[V]} \geq \delta$ , there exists a polynomial sequence $P \colon V \to \mathbb{R}/\mathbb{Z}$ such that

\left| \frac{1}{|V|} \sum_{x \in V} f(x) e(-P(x) \right| \geq c ,

where $e(x) := e^{2 \pi i x}$ . This conjecture was proved to be true by Tao and Ziegler.

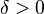The Inverse Conjecture for Gowers $U^{d}[N]$ norm asserts that for any $\delta > 0$ , a finite collection of (d-1)-step nilmanifolds 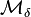$\mathcal{M}_\delta$ and constants $c ,C$ can be found, so that the following is true. 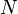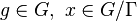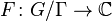If $N$ is a positive integer and $f\colon [N]\to \mathbb{C}$ is bounded in absolute value by 1 and $\Vert f \Vert_{U^{d}[N]} \geq \delta$ , then there exists a nilmanifold $G/\Gamma \in \mathcal{M}_\delta$ and a nilsequence $F(g^nx)$ where $g \in G,\ x \in G/\Gamma$ and $F\colon G/\Gamma \to \mathbb{C}$ bounded by 1 in absolute value and with Lipschitz constant bounded by $C$ such that:

\left| \frac{1}{N} \sum_{n =0}^{N-1} f(n) \overline{ F(g^nx}) \right| \geq c .

This conjecture was proved to be true by Green, Tao and Ziegler . It should be stressed that the appearance of nilsequences in the above statement is necessary. The statement is no longer true if we only consider polynomial phases.

References

Tao, Terence (2012). Higher order Fourier analysis. Graduate Studies in Mathematics 142. Providence, RI: American Mathematical Society. ISBN 978-0-8218-8986-2. Zbl 1277.11010.

Green, B.; Tao, T.; Ziegler, T. (2012). "An inverse theorem for the Gowers U^(s+1)[N]-norm". Annals of Mathematics 176 (2): 1231. doi:10.4007/annals.2012.176.2.11.

Tao, T.; Ziegler, T. (2011). "The Inverse Conjecture for the Gowers Norm over Finite Fields in Low Characteristic". Annals of Combinatorics 16: 121. doi:10.1007/s00026-011-0124-3.