Gopakumar–Vafa invariant

In theoretical physics Rajesh Gopakumar and Cumrun Vafa introduced new topological invariants, which named Gopakumar–Vafa invariant, that represent the number of BPS states on Calabi–Yau 3-fold, in a series of papers. (see Gopakumar & Vafa (1998a),Gopakumar & Vafa (1998b) and also see Gopakumar & Vafa (1998c), Gopakumar & Vafa (1998d).)　They lead the following formula generating function for the Gromov–Witten invariant on Calabi–Yau 3-fold M.

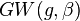\sum_{g\ge0,n\ge1,\beta\in H^2(M,\mathbb{Z})} GW(g,\beta)q^{-\beta}\lambda^{2g-2}=\sum_{k>0,r\ge0,\beta\in H^2(M,\mathbb{Z})}BPS(r,\beta)\frac{1}{k}\left(2\sin\left(\frac{k\lambda}{2}\right)^{2r-2}q^{k\beta}\right)

where GW(g,\beta) is Gromov–Witten invariant, 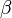\beta the number of pseudoholomorphic curves with genus g and 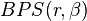BPS(r,\beta) the number of the BPS states.

As a partition function in topological quantum field theory

Gopakumar–Vafa invariants can be viewed as a partition function in topological quantum field theory.　They are proposed to be the partition function in Gopakumar–Vafa form:

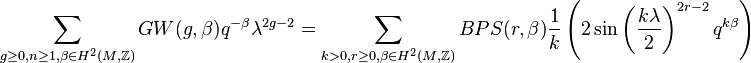
Z_{top}=\exp\left[\sum_{\begin{smallmatrix} k>0,\ r\ge0,\\ \beta\in H^2(M,\mathbb{Z})\end{smallmatrix}}BPS(r,\beta)\frac{1}{k}\left(2\sin\left(\frac{k\lambda}{2}\right)^{2r-2}q^{k\beta\cdot t}\right)\right]\ .

References