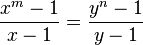Goormaghtigh conjecture

In mathematics, the Goormaghtigh conjecture is a conjecture in number theory named for the Belgian mathematician René Goormaghtigh. The conjecture is that the only non-trivial integer solutions of the exponential Diophantine equation

satisfying x > y > 1 and n, m > 2 are

• (x, y, m, n) = (5, 2, 3, 5); and
• (x, y, m, n) = (90, 2, 3, 13).

This may be expressed as saying that 31 and 8191 are the only two numbers that are repunits with at least 3 digits in two different bases.

Balasubramanian and Shorey proved in 1980 that there are only finitely many possible solutions to the equations in (x,y,m,n) with prime divisors of x and y lying in a given finite set and that they may be effectively computed.

See also

• Feit–Thompson conjecture

References

• Goormaghtigh, Rene. L’Intermédiaire des Mathématiciens 24 (1917), 88

• Bugeaud, Y.; Shorey, T.N. (2002). "On the diophantine equation (x^m - 1)/(x-1) = (y^n - 1)/(y-1)" (PDF). Pacific Journal of Mathematics 207 (1): 61–75. 

• Balasubramanian, R.; Shorey, T.N. (1980). "On the equation a(x^m − 1)/(x − 1) = b(yⁿ − 1)/(y − 1)". Mathematica Scandinavica 46: 177–182. Zbl 0434.10013. 
• Guy, Richard K. (2004). Unsolved Problems in Number Theory (3rd ed.). Springer-Verlag. p. 242. ISBN 0-387-20860-7. Zbl 1058.11001. 
• Nesterenko, Yu. V.; Shorey, T. N. (1998). "On an equation of Goormaghtigh" (PDF). Acta Arithmetica. LXXXIII (4): 381–389. Zbl 0896.11010. 
• Shorey, T.N.; Tijdeman, R. (1986). Exponential Diophantine equations. Cambridge Tracts in Mathematics 87. Cambridge University Press. pp. 203–204. ISBN 0-521-26826-5. Zbl 0606.10011.