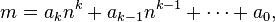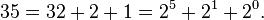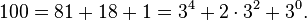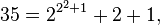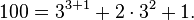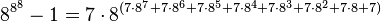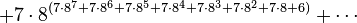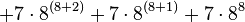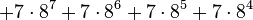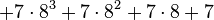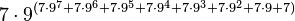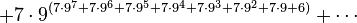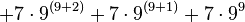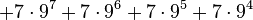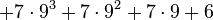Goodstein's theorem
In mathematical logic, Goodstein's theorem is a statement about the natural numbers, proved by Reuben Goodstein in 1944, which states that every Goodstein sequence eventually terminates at 0. Kirby and Paris[1] showed that it is unprovable in Peano arithmetic (but it can be proven in stronger systems, such as second order arithmetic). This was the third "natural" example of a true statement that is unprovable in Peano arithmetic (after Gerhard Gentzen's 1943 direct proof of the unprovability of ε0-induction in Peano arithmetic and the Paris–Harrington theorem). Earlier statements of this type had either been, except for Gentzen, extremely complicated, ad-hoc constructions (such as the statements generated by the construction given in Gödel's incompleteness theorem) or concerned metamathematics or combinatorial results.[1]
Laurence Kirby and Jeff Paris introduced a graph theoretic hydra game with behavior similar to that of Goodstein sequences: the "Hydra" is a rooted tree, and a move consists of cutting off one of its "heads" (a branch of the tree), to which the hydra responds by growing a finite number of new heads according to certain rules. Kirby and Paris proved that the Hydra will eventually be killed, regardless of the strategy that Hercules uses to chop off its heads, though this may take a very, very, very long time.[1]
Hereditary base-n notation
Goodstein sequences are defined in terms of a concept called "hereditary base-n notation". This notation is very similar to usual base-n positional notation, but the usual notation does not suffice for the purposes of Goodstein's theorem.
In ordinary base-n notation, where n is a natural number greater than 1, an arbitrary natural number m is written as a sum of multiples of powers of n:
where each coefficient 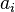 satisfies
satisfies 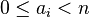 , and
, and 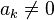 . For example, in base 2,
. For example, in base 2,
Thus the base 2 representation of 35 is 100011, which means 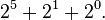 Similarly, 100 represented in base 3 is 10201:
Similarly, 100 represented in base 3 is 10201:
Note that the exponents themselves are not written in base-n notation. For example, the expressions above include 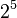 and
and 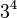 .
.
To convert a base-n representation to hereditary base n notation, first rewrite all of the exponents in base-n notation. Then rewrite any exponents inside the exponents, and continue in this way until every digit appearing in the expression is n or less.
For example, while 35 in ordinary base-2 notation is 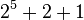 , it is written in hereditary base-2 notation as
, it is written in hereditary base-2 notation as
using the fact that 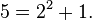 Similarly, 100 in hereditary base 3 notation is
Similarly, 100 in hereditary base 3 notation is
Goodstein sequences
The Goodstein sequence G(m) of a number m is a sequence of natural numbers. The first element in the sequence G(m) is m itself. To get the second, G(m)(2), write m in hereditary base 2 notation, change all the 2s to 3s, and then subtract 1 from the result. In general, the 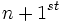 term G(m)(n+1) of the Goodstein sequence of m is as follows:
take the hereditary base n+1 representation of G(m)(n), and
replace each occurrence of the base n+1 with n+2 and then
subtract one. Note that the next term depends both on the previous term
and on the index n. Continue until the result is zero, at which point the sequence terminates.
term G(m)(n+1) of the Goodstein sequence of m is as follows:
take the hereditary base n+1 representation of G(m)(n), and
replace each occurrence of the base n+1 with n+2 and then
subtract one. Note that the next term depends both on the previous term
and on the index n. Continue until the result is zero, at which point the sequence terminates.
Early Goodstein sequences terminate quickly. For example, G(3) terminates at the sixth step:
| Base | Hereditary notation | Value | Notes |
|---|---|---|---|
| 2 | 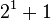 | 3 | Write 3 in base 2 notation |
| 3 | 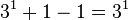 | 3 | Switch the 2 to a 3, then subtract 1 |
| 4 | 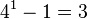 | 3 | Switch the 3 to a 4, then subtract 1. Now there are no more 4s left |
| 5 | 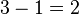 | 2 | No 4s left to switch to 5s. Just subtract 1 |
| 6 | 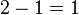 | 1 | No 5s left to switch to 6s. Just subtract 1 |
| 7 | 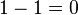 | 0 | No 6s left to switch to 7s. Just subtract 1 |
Later Goodstein sequences increase for a very large number of steps. For example, G(4) ![]() A056193 starts as follows:
A056193 starts as follows:
| Hereditary notation | Value |
|---|---|
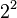 | 4 |
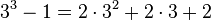 | 26 |
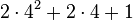 | 41 |
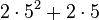 | 60 |
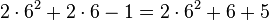 | 83 |
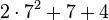 | 109 |
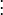 | 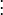 |
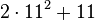 | 253 |
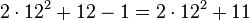 | 299 |
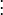 | 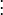 |
Elements of G(4) continue to increase for a while, but at base 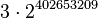 ,
they reach the maximum of
,
they reach the maximum of 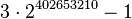 , stay there for the next
, stay there for the next 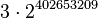 steps, and then begin their first and final descent.
steps, and then begin their first and final descent.
The value 0 is reached at base 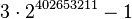 . (Curiously, this is a Woodall number:
. (Curiously, this is a Woodall number: 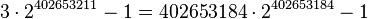 . This is also the case with all other final bases for starting values greater than 4.)
. This is also the case with all other final bases for starting values greater than 4.)
However, even G(4) doesn't give a good idea of just how quickly the elements of a Goodstein sequence can increase. G(19) increases much more rapidly, and starts as follows:
| Hereditary notation | Value |
|---|---|
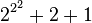 | 19 |
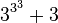 | 7,625,597,484,990 |
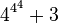 | 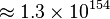 |
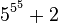 | 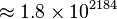 |
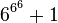 | 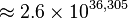 |
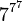 | 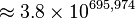 |
|
|
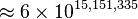 |
|
|
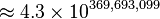 |
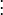 | 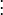 |
In spite of this rapid growth, Goodstein's theorem states that every Goodstein sequence eventually terminates at 0, no matter what the starting value is.
Proof of Goodstein's theorem
Goodstein's theorem can be proved (using techniques outside Peano arithmetic, see below) as follows: Given a Goodstein sequence G(m), we construct a parallel sequence P(m) of ordinal numbers which is strictly decreasing and terminates. Then G(m) must terminate too, and it can terminate only when it goes to 0. A common misunderstanding of this proof is to believe that G(m) goes to 0 because it is dominated by P(m). In fact that P(m) dominates G(m) plays no role at all. The important points is: G(m)(k) exists if and only if P(m)(k) exists (parallelism). Then if P(m) terminates, so does G(m). And G(m) can terminate only when it comes to 0.
More precisely, each term P(m)(n) of the sequence P(m) is obtained by applying a function f on the term G(m)(n) of the Goodstein sequence of m as follows: take the hereditary base n+1 representation of G(m)(n), and replace each occurrence of the base n+1 with the first infinite ordinal number ω. For example 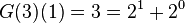 and
and 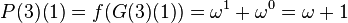 . Addition, multiplication and exponentiation of ordinal numbers are well defined.
. Addition, multiplication and exponentiation of ordinal numbers are well defined.
- The base-changing operation of the Goodstein sequence when going from G(m)(n) to G(m)(n+1) does not change the value of f (that's the main point of the construction), thus after the minus 1 operation, P(m)(n+1) will be strictly smaller than P(m)(n). For example,
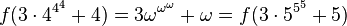 , hence
, hence 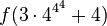 is strictly greater than
is strictly greater than 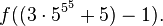
If the sequence G(m) did not go to 0, it would not terminate and would be infinite (since G(m)(k+1) would always exist). Consequently, P(m) also would be infinite (since in its turn P(m)(k+1) would always exist too). But P(m) is strictly decreasing and the standard order < on ordinals is well-founded, therefore an infinite strictly decreasing sequence cannot exist, or equivalently, every strictly decreasing sequence of ordinals does terminate (and cannot be infinite). This contradiction shows that G(m) terminates, and since it terminates, goes to 0 (by the way, since there exists a natural number k such that G(m)(k)=0, by construction of P(m) we have that P(m)(k)=0).
While this proof of Goodstein's theorem is fairly easy, the Kirby–Paris theorem which says that Goodstein's theorem is not a theorem of Peano arithmetic, is technical and considerably more difficult. It makes use of countable nonstandard models of Peano arithmetic. What Kirby showed is that Goodstein's theorem leads to Gentzen's theorem, i.e. it can substitute for induction up to ε0.
Extended Goodstein's theorem
Suppose the definition Goodstein sequence is changed so that instead of
replacing each occurrence of the base b with b+1
it was replaces it with b+2. Would the sequence still terminate?
More generally, let 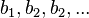 be any sequences of
integers.
Then let the
be any sequences of
integers.
Then let the 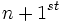 term G(m)(n+1) of the extended Goodstein sequence of m be as
follows: take the hereditary base
term G(m)(n+1) of the extended Goodstein sequence of m be as
follows: take the hereditary base 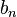 representation of
G(m)(n), and replace each occurrence of the base
representation of
G(m)(n), and replace each occurrence of the base 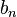 with
with 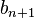 and then subtract one.
The claim is that this sequence still terminates.
The extended proof defines
and then subtract one.
The claim is that this sequence still terminates.
The extended proof defines 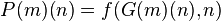 as
follows: take the hereditary base
as
follows: take the hereditary base 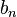 representation of
representation of
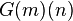 , and replace each occurrence of the base
, and replace each occurrence of the base
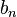 with the first infinite ordinal number
with the first infinite ordinal number 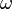 .
The base-changing operation of the Goodstein sequence when going
from G(m)(n) to G(m)(n+1) still does not change the value of f.
For example, if
.
The base-changing operation of the Goodstein sequence when going
from G(m)(n) to G(m)(n+1) still does not change the value of f.
For example, if 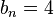 and if
and if 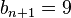 ,
then
,
then
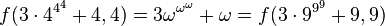 , hence the ordinal
, hence the ordinal 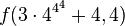 is strictly greater than the ordinal
is strictly greater than the ordinal 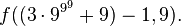
Sequence length as a function of the starting value
The Goodstein function, 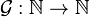 , is defined such that
, is defined such that 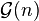 is the length of the Goodstein sequence that starts with n. (This is a total function since every Goodstein sequence terminates.) The extreme growth-rate of
is the length of the Goodstein sequence that starts with n. (This is a total function since every Goodstein sequence terminates.) The extreme growth-rate of 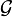 can be calibrated by relating it to various standard ordinal-indexed hierarchies of functions, such as the functions
can be calibrated by relating it to various standard ordinal-indexed hierarchies of functions, such as the functions 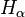 in the Hardy hierarchy, and the functions
in the Hardy hierarchy, and the functions 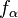 in the fast-growing hierarchy of Löb and Wainer:
in the fast-growing hierarchy of Löb and Wainer:
- Kirby and Paris (1982) proved that
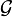 has approximately the same growth-rate as
has approximately the same growth-rate as 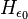 (which is the same as that of
(which is the same as that of 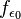 ); more precisely,
); more precisely, 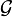 dominates
dominates 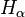 for every
for every 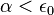 , and
, and 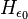 dominates
dominates 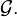
- (For any two functions
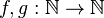 ,
,  is said to dominate
is said to dominate 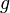 if
if 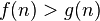 for all sufficiently large
for all sufficiently large 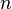 .)
.)
- Cichon (1983) showed that
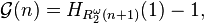
- where
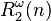 is the result of putting n in hereditary base-2 notation and then replacing all 2s with ω (as was done in the proof of Goodstein's theorem).
is the result of putting n in hereditary base-2 notation and then replacing all 2s with ω (as was done in the proof of Goodstein's theorem).
- Caicedo (2007) showed that if
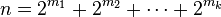 with
with 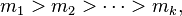 then
then
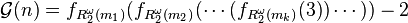 .
.
Some examples:
| n | 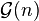 | ||||
|---|---|---|---|---|---|
| 1 | 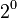 |
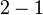 |
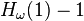 |
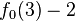 |
2 |
| 2 | 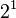 |
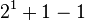 |
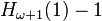 |
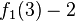 |
4 |
| 3 | 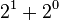 |
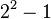 |
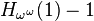 |
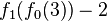 |
6 |
| 4 | 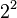 |
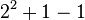 |
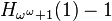 |
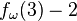 |
3·2402653211 − 2 |
| 5 | 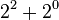 |
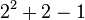 |
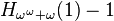 |
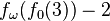 |
> A(4,4) |
| 6 | 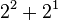 |
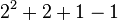 |
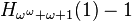 |
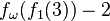 |
> A(6,6) |
| 7 | 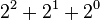 |
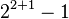 |
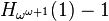 |
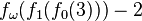 |
> A(8,8) |
| 8 | 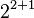 |
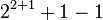 |
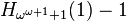 |
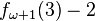 |
> A3(3,3) = A(A(61, 61), A(61, 61)) |
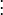 | |||||
| 12 | 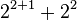 |
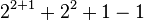 |
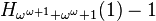 |
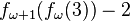 |
> fω+1(64) > Graham's number |
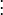 | |||||
| 19 | 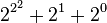 |
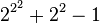 |
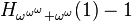 |
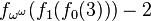 |
|
(For Ackermann function and Graham's number bounds see fast-growing hierarchy#Functions in fast-growing hierarchies.)
Application to computable functions
Goodstein's theorem can be used to construct a total computable function that Peano arithmetic cannot prove to be total. The Goodstein sequence of a number can be effectively enumerated by a Turing machine; thus the function which maps n to the number of steps required for the Goodstein sequence of n to terminate is computable by a particular Turing machine. This machine merely enumerates the Goodstein sequence of n and, when the sequence reaches 0, returns the length of the sequence. Because every Goodstein sequence eventually terminates, this function is total. But because Peano arithmetic does not prove that every Goodstein sequence terminates, Peano arithmetic does not prove that this Turing machine computes a total function.
See also
- Non-standard model of arithmetic
- Fast-growing hierarchy
- Paris–Harrington theorem
- Kanamori–McAloon theorem
- Kruskal's tree theorem
References
- ↑ 1.0 1.1 1.2 Kirby, L.; Paris, J. (1982). "Accessible Independence Results for Peano Arithmetic". Bulletin of the London Mathematical Society 14 (4): 285. doi:10.1112/blms/14.4.285.
Bibliography
- Goodstein, R. (1944), "On the restricted ordinal theorem", Journal of Symbolic Logic 9: 33–41, JSTOR 2268019.
- Cichon, E. (1983), "A Short Proof of Two Recently Discovered Independence Results Using Recursive Theoretic Methods", Proceedings of the American Mathematical Society 87: 704–706, JSTOR 2043364.
- Caicedo, A. (2007), "Goodstein's function", Revista Colombiana de Matemáticas 41 (2): 381–391.
External links
- Weisstein, Eric W., "Goodstein Sequence", MathWorld.
- Some elements of a proof that Goodstein's theorem is not a theorem of PA, from an undergraduate thesis by Justin T Miller
- A Classification of non standard models of Peano Arithmetic by Goodstein's theorem - Thesis by Dan Kaplan, Franklan and Marshall College Library
- Definitions of Goodstein sequences in the programming languages Ruby and Haskell, as well as a large-scale plot
- The Hydra game implemented as a Java applet
- Goodstein Sequences: The Power of a Detour via Infinity - good exposition with illustrations of Goodstein Sequences and the hydra game.