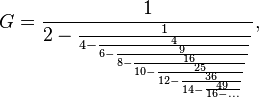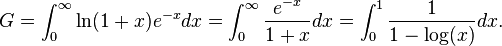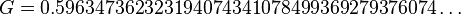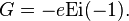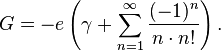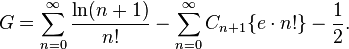Gompertz constant

In mathematics, the Gompertz constant or Euler-Gompertz constant, denoted by G, appears in integral evaluations and as a value of special functions. It is named after B. Gompertz.

It can be defined by the continued fraction

G = \frac{1}{2-\frac{1}{4-\frac{4}{6-\frac{9}{8-\frac{16}{10-\frac{25}{12-\frac{36}{14-\frac{49}{16-\dots}}}}}}}} ,

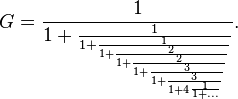
or, alternatively, by

G = \frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{2}{1+\frac{2}{1+\frac{3}{1+\frac{3}{1+4 \frac{1}{1+\dots}}}}}}}}.

The most frequent appearance of G is in the following integrals:

G = \int_0^\infty\ln(1+x)e^{-x}dx=\int_0^\infty\frac{e^{-x}}{1+x}dx=\int_0^1\frac{1}{1-\log(x)}dx.

The numerical value of G is about

G = 0.596347362323194074341078499369279376074\dots

During the studying divergent infinite series Euler met with G via, for example, the above integral representations. Le Lionnais called G as Gompertz constant by its role in survival analysis.[1]

Identities involving the Gompertz constant

The constant G can be expressed by the exponential integral as

G = -e\textrm{Ei}(-1).

Applying the Taylor expansion of 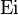\textrm{Ei} we have that

G = -e\left(\gamma+\sum_{n=1}^\infty\frac{(-1)^n}{n\cdot n!}\right).

Gompertz's constant is connected to the Gregory coefficients via the 2013 formula of I. Mező:[2]

G = \sum_{n=0}^\infty\frac{\ln(n+1)}{n!}-\sum_{n=0}^\infty C_{n+1}\{e\cdot n!\}-\frac{1}{2}.

External links

Notes

  1. ↑ Steven R., Finch (2003). Mathematical Constants. Cambridge University Press. pp. 425–426.
  2. ↑ Mező, István (2013). "Gompertz constant, Gregory coefficients and a series of the logarithm function". Journal of Analysis and Number Theory (7): 1–4.