Gomory–Hu tree
In combinatorial optimization, the Gomory–Hu tree[1] of an undirected graph with capacities is a weighted tree that represents the minimum s-t cuts for all s-t pairs in the graph. The Gomory–Hu tree can be constructed in | V | − 1 minimum cut computations.
Definition
Let G = ((VG, EG), c) be an undirected graph with c(u,v) being the capacity of the edge (u,v) respectively.
- Denote the minimum capacity of an s-t cut by λst for each s, t ∈ VG.
- Let T = (VT,ET) be a tree with VT = VG, denote the set of edges in an s-t path by Pst for each s,t ∈ VT.
Then T is said to be a Gomory–Hu tree of G if
- λst = mine∈Pst c(Se, Te) for all s, t ∈ VG,
where
- Se and Te are the two connected components of T∖{e} in the sense that (Se, Te) form a s-t cut in G, and
- c(Se, Te) is the capacity of the cut in G.
Algorithm
Gomory–Hu Algorithm
- Input: A weighted undirected graph G = ((VG, EG), c).
- Output: A Gomory–Hu Tree T = (VT, ET).
- 1. Set VT = {VG} and ET = ∅.
- 2. Choose some X∈VT with | X | ≥ 2 if such X exists. Otherwise, go to step 6.
- 3. For each connected component C = (VC, EC) in T∖X. Let SC = ∪vT∈VC vT. Let S = { SC | C is a connected component in T∖X}.
- Contract the components to form G' = ((VG', EG'), c'), where
- VG' = X ∪ S.
- EG' = EG|X×X ∪ {(u, SC) ∈ X×S | (u,v)∈EG for some v∈SC}.
- c' : VG'×VG'→R+ is the capacity function defined as,
- if (u,SC)∈EG|X×S, c'(u,SC) = Σv∈SC:(u,v)∈EGc(u,v),
- c'(u,v) = c(u,v) otherwise.
- 4. Choose two vertices s, t ∈ X and find a minimum s-t cut (A',B') in G'.
- Set A = (∪SC∈A'∩S SC) ∪ (A' ∩ X) and B = (∪SC∈B'∩S SC) ∪ (B' ∩ X).
- 5. Set VT = (VT∖X) ∪ {A ∩ X, B ∩ X}.
- For each e = (X, Y) ∈ ET do
- If Y⊂A, set e' = (A ∩ X, Y), else set e' = (B ∩ X, Y).
- Set ET = (ET∖{e}) ∪ {e'} and w(e') = w(e).
- Set ET = ET ∪ {(A∩X, B∩X)}.
- Set w((A∩X, B∩X)) = c'(A', B').
- Go to step 2.
- 6. Replace each {v} ∈ VT by v and each ({u},{v}) ∈ ET by (u,v). Output T.
Analysis
Using the submodular property of the capacity function c, one has
- c(X) + c(Y) ≥ c(X ∩ Y) + c(X ∪ Y).
Then it can be shown that the minimum s-t cut in G' is also a minimum s-t cut in G for any s, t ∈ X.
To show that for all (P, Q) ∈ ET, w(P,Q) = λpq for some p ∈ P, q ∈ Q throughout the algorithm, one makes use of the following Lemma,
- For any i, j, k in VG, λik ≥ min(λij, λjk).
The Lemma can be used again repeatedly to show that the output T satisfies the properties of a Gomory–Hu Tree.
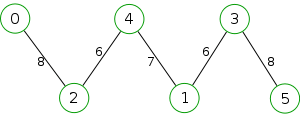
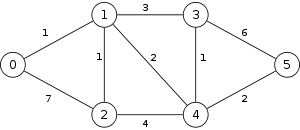
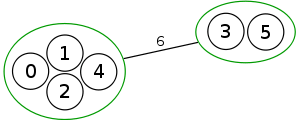
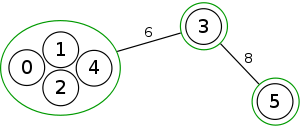
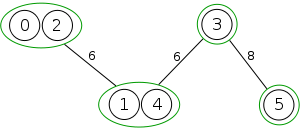
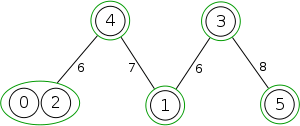
Example
The following is a simulation of the Gomory–Hu's algorithm, where
- green circles are vertices of T.
- red and blue circles are the vertices in G'.
- grey vertices are the chosen s and t.
- red and blue coloring represents the s-t cut.
- dashed edges are the s-t cut-set.
- A is the set of vertices circled in red and B is the set of vertices circled in blue.
| G' | T | |
|---|---|---|
 |
 | |
| ||
| 1. | 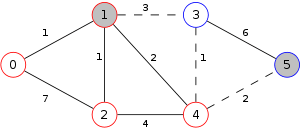 |
 |
| ||
| 2. |  |
 |
| ||
| 3. |  |
 |
| ||
| 4. | 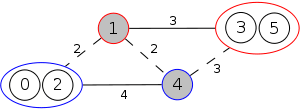 |
 |
| ||
| 5. | 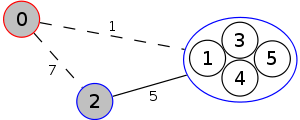 |
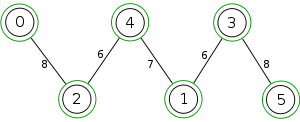 |
| ||
| 6. |
| |
| ||
Implementations: Sequential and Parallel
The Gusfield's algorithm can be used to find a Gomory–Hu tree without any vertex contraction in the same running time-complexity, which simplifies the implementation of constructing a Gomory–Hu Tree.
Andrew V. Goldberg and K. Tsioutsiouliklis implemented the Gomory-Hu algorithm and Gusfield algorithm. Experimental results comparing these algorithms are reported in[2] Source code is available here.
Cohen et al.[3] reports results on two parallel implementations of Gusfield's algorithm using OpenMP and MPI, respectively. Source code of these implementations is available here: Parallel Cut Tree Algorithms Page.
History
The Gomory–Hu tree was introduced by R. E. Gomory and T. C. Hu in 1961.
See also
References
- ↑ Gomory, R. E.; Hu, T. C. (1961). "Multi-terminal network flows". Journal of the Society for Industrial and Applied Mathematics 9.
- ↑ Goldberg, A. V.; Tsioutsiouliklis, K. (2001). "Cut Tree Algorithms: An Experimental Study". Journal of Algorithms 38 (1): 51–83. doi:10.1006/jagm.2000.1136.
- ↑ Cohen, J.; L. A. Rodrigues, F. Silva, R. Carmo, A. Guedes, E. P. Duarte Jr. (2011). "Parallel Implementations of Gusfield's Cut Tree Algorithm". Lecture Notes in Computer Science (LNCS). 7016 (Springer) (11th International Conference Algorithms and Architectures for Parallel Processing (ICA3PP)). ISSN 0302-9743.
- Dan Gusfield (1990). "Very Simple Methods for All Pairs Network Flow Analysis". SIAM J. Comput. 19 (1): 143–155. doi:10.1137/0219009.
- B. H. Korte, Jens Vygen (2008). "8.6 Gomory–Hu Trees". Combinatorial Optimization: Theory and Algorithms (Algorithms and Combinatorics, 21). Springer Berlin Heidelberg. pp. 180–186. ISBN 978-3-540-71844-4.