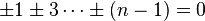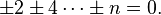Golygon

An example of a simple 8-sided golygon

A golygon is any polygon with all right angles, whose sides are consecutive integer lengths. Golygons were invented and named by Lee Sallows, and popularized by A.K. Dewdney in a 1990 Scientific American column (Smith).[1] Variations on the definition of golygons involve allowing edges to cross, using sequences of edge lengths other than the consecutive integers, and considering turn angles other than 90°.[2]

In any golygon, all horizontal edges have the same parity as each other, as do all vertical edges. Therefore, the number n of sides must allow the solution of the system of equations

\pm 1 \pm 3\cdots \pm (n-1) = 0
\pm 2 \pm 4\cdots \pm n = 0.

It follows from this that n must be a multiple of 8. Thus the number of golygons for n = 1, 2, 3, 4, ... is 4, 112, 8432, 909288, etc.[3]

The number of solutions to this system of equations may be computed efficiently using generating functions (sequence A007219 in OEIS) but finding the number of solutions that correspond to non-crossing golygons seems to be significantly more difficult.

There is a unique eight-sided golygon (shown in the figure); it can tile the plane by 180-degree rotation using the Conway criterion.

Generalizations

A serial-sided isogon of order n is a closed polygon with a constant angle at each vertex and having consecutive sides of length 1, 2, ..., n units. The polygon may be self-crossing.[4] Golygons are a special case of Serial-sided isogons.[5]

The three-dimensional generalization of a golygon is called a golyhedron–a closed simply-connected solid figure confined to the faces of a cubical lattice and having face areas in the sequence 1, 2, ..., n, for some integer n.[6] Golyhedrons have been found with values of n equal to 32, 15, 12, and 11 (the mininum possible).[7]

See also

References

  1. ↑ Dewdney, A.K. (1990). "An odd journey along even roads leads to home in Golygon City". Scientific American 263: 118–121.
  2. ↑ Harry J. Smith. "What is a Golygon?". Archived from the original on 2009-10-27.
  3. ↑ Weisstein, Eric W., "Golygon", MathWorld.
  4. ↑ Sallows, Lee (1992). "New pathways in serial isogons". The Mathematical Intelligencer 14 (2): 55–67. doi:10.1007/BF03025216.
  5. ↑ Sallows, Lee; Gardner, Martin; Guy, Richard K.; Knuth, Donald (1991). "Serial isogons of 90 degrees". Mathematics Magazine 64 (5): 315–324. doi:10.2307/2690648. JSTOR 2690648.
  6. ↑ Golygons and golyhedra
  7. ↑ Golyhedron update

External links