Glossary of category theory
This is a glossary of properties and concepts in category theory in mathematics.
Categories
A category A is said to be:
- small if the class of all morphisms is a set (i.e., not a proper class); otherwise large.
- locally small if the morphisms between every pair of objects A and B form a set.
- Some authors assume a foundation in which the collection of all classes forms a "conglomerate", in which case a quasicategory is a category whose objects and morphisms merely form a conglomerate.[1] (NB other authors use the term "quasicategory" with a different meaning.[2])
- isomorphic to a category B if there is an isomorphism between them.
- equivalent to a category B if there is an equivalence between them.
- concrete if there is a faithful functor from A to Set; e.g., Vec, Grp and Top.
- discrete if each morphism is an identity morphism (of some object).
- thin category if there is at most one morphism between any pair of objects.
- a subcategory of a category B if there is an inclusion functor given from A to B.
- a full subcategory of a category B if the inclusion functor is full.
- wellpowered if for each object A there is only a set of pairwise non-isomorphic subobjects.
- complete if all small limits exist.
- cartesian closed if it has a terminal object and that any two objects have a product and exponential.
- abelian if it has a zero object, it has all pullbacks and pushouts, and all monomorphisms and epimorphisms are normal.
- normal if every monic is normal.[3]
- balanced if every bimorphism is an isomorphism.
- preadditive if it is enriched over the monoidal category of abelian groups. More generally, it is R-linear if it is enriched over the monoidal category of R-modules, for R a commutative ring.
- additive if it is preadditive and admits all finitary biproducts.
- skeletal if isomorphic objects are necessarily identical.
Morphisms
A morphism f in a category is called:
- an epimorphism if
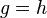whenever 
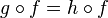. In other words, f is the dual of a monomorphism. - an identity if f maps an object A to A and for any morphisms g with domain A and h with codomain A,
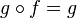and 
. - an 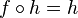inverse to a morphism g if
is defined and is equal to the identity morphism on the codomain of g, and 
is defined and equal to the identity morphism on the domain of g. The inverse of g is unique and is denoted by g−1. f is a left inverse to g if is defined and is equal to the identity morphism on the domain of g, and similarly for a right inverse. - an isomorphism if there exists an inverse of f.
- a monomorphism (also called monic) if 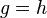whenever
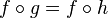; e.g., an injection in Set. In other words, f is the dual of an epimorphism. - a bimorphism is a morphism that is both an epimorphism and a monomorphism.
- a retraction if it has a right inverse.
- a coretraction if it has a left inverse.
Functors
A functor F is said to be:
- a constant if F maps every object in a category to the same object A and every morphism to the identity on A.
- faithful if F is injective when restricted to each hom-set.
- full if F is surjective when restricted to each hom-set.
- isomorphism-dense (sometimes called essentially surjective) if for every B there exists A such that F(A) is isomorphic to B.
- an equivalence if F is faithful, full and isomorphism-dense.
- amnestic provided that if k is an isomorphism and F(k) is an identity, then k is an identity.
- reflect identities provided that if F(k) is an identity then k is an identity as well.
- reflect isomorphisms provided that if F(k) is an isomorphism then k is an isomorphism as well.
Objects
An object A in a category is said to be:
- isomorphic to an object B if there is an isomorphism between A and B.
- initial if there is exactly one morphism from A to each object B; e.g., empty set in Set.
- terminal if there is exactly one morphism from each object B to A; e.g., singletons in Set.
- a zero object if it is both initial and terminal, such as a trivial group in Grp.
An object A in an abelian category is:
- simple if it is not isomorphic to the zero object and any subobject of A is isomorphic to zero or to A.
- finite length if it has a composition series. The maximum number of proper subobjects in any such composition series is called the length of A.[4]
Notes
- ↑ Adámek, Jiří; Herrlich, Horst, and Strecker, George E (2004) [1990]. Abstract and Concrete Categories (The Joy of Cats) (PDF). New York: Wiley & Sons. p. 40. ISBN 0-471-60922-6.
- ↑ Joyal, A. (2002). "Quasi-categories and Kan complexes". Journal of Pure and Applied Algebra 175 (1-3): 207–222. doi:10.1016/S0022-4049(02)00135-4.
- ↑ http://planetmath.org/encyclopedia/NormalCategory.html
- ↑ Kashiwara & Schapira 2006, exercise 8.20
References
- Kashiwara, Masaki; Schapira, Pierre (2006). "Categories and sheaves"
- Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics 5 (2nd ed.). New York, NY: Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001.
- Pedicchio, Maria Cristina; Tholen, Walter, eds. (2004). Categorical foundations. Special topics in order, topology, algebra, and sheaf theory. Encyclopedia of Mathematics and Its Applications 97. Cambridge: Cambridge University Press. ISBN 0-521-83414-7. Zbl 1034.18001.