Giuseppe Vitali
| Giuseppe Vitali | |
|---|---|
 | |
| Born |
26 August 1875 Ravenna, Italy |
| Died |
29 February 1932 (aged 56) Bologna, Italy |
| Nationality | Italian |
| Fields | Mathematics |
Giuseppe Vitali (26 August 1875 – 29 February 1932) was an Italian mathematician who worked in several branches of mathematical analysis.
Mathematical contributions
Vitali was the first to give an example of a non-measurable subset of real numbers, see Vitali set. His covering theorem is a fundamental result in measure theory. He also proved several theorems concerning convergence of sequences of measurable and holomorphic functions. Vitali convergence theorem generalizes Lebesgue's dominated convergence theorem. Another theorem bearing his name gives a sufficient condition for the uniform convergence of a sequence of holomorphic functions on an open domain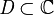 
to a holomorphic function on 
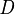. This result has been generalized to normal families of meromorphic functions, holomorphic functions of several complex variables, and so on.
In the last part of his life, he also worked on absolute differential calculus and on the geometry of Hilbert spaces.[1][2]
See also
- Vitali convergence theorem
- Vitali covering theorem
- Vitali-Hahn-Saks theorem
- Vitali set
Bibliography
- Tonolo, Angelo (1932), "Commemorazione di Giuseppe Vitali (Commemoration of Giuseppe Vitali)", Rendiconti del Seminario Matematico della Università di Padova 3: 67–81, JFM 58.0049.10, (in Italian). Available at Numdam.
- Tricomi, G. F. (1962), "Matematici italiani del primo secolo dello stato unitario (Italian mathematicians of the first century of the unitary state)", Memorie dell'Accademia delle Scienze di Torino. Classe di Scienze fisiche matematiche e naturali, series IV I: 120, Zbl 0132.24405
|chapter=ignored (help) (in Italian). Available from the website of the Società Italiana di Storia delle Matematiche.
References
- Vitali, Giuseppe (1908) [17 december 1907], "Sui gruppi di punti e sulle funzioni di variabili reali", Atti dell'Accademia delle Scienze di Torino (in Italian) 43: 75–92, JFM 39.0101.05, archived from the original on 2009-03-31. "On groups of points and functions of real variables" (English translation of the title) is the paper where the first proof of Vitali covering theorem is given.
Notes
- ↑ G. Vitali, Una derivazione covariante formata coll’ausilio di n sistemi covarianti del 1 ordine, Atti della Soc. Linguistica di Sc. e Lett. 2 (1924), 248-253.
- ↑ G. Vitali, Intorno ad una derivazione nel calcolo assoluto, Atti della Soc. Linguistica di Sc. e Lett. 4 (1925), 287-291.
External links
- O'Connor, John J.; Robertson, Edmund F., "Giuseppe Vitali", MacTutor History of Mathematics archive, University of St Andrews.
|