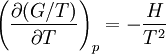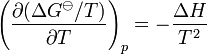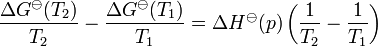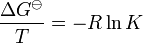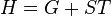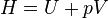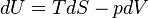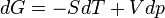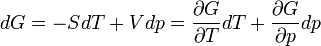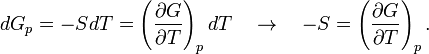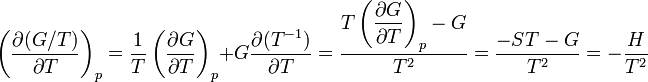Gibbs–Helmholtz equation

The Gibbs–Helmholtz equation is a thermodynamic equation used for calculating changes in the Gibbs energy of a system as a function of temperature. It is named after Josiah Willard Gibbs and Hermann von Helmholtz.

Equation

The equation is:[1]

\left( \frac{\partial (G/T) } {\partial T} \right)_p = - \frac {H} {T^2}

where H is the enthalpy, T the absolute temperature and G the Gibbs free energy of the system, all at constant pressure p. The equation states that the change in the G/T ratio at constant pressure as a result of an infinitesimally small change in temperature is a factor H/T2.

Chemical reactions

Main article: Thermochemistry

The typical applications are to chemical reactions. The equation reads:[2]

\left( \frac{\partial ( \Delta G^\ominus/T ) } {\partial T} \right)_p = - \frac {\Delta H} {T^2}

with ΔG as the change in Gibbs energy and ΔH as the enthalpy change (considered independent of temperature). The o denotes standard pressure (1 bar).

Integrating with respect to T (again p is constant) it becomes:

\frac{\Delta G^\ominus(T_2)}{T_2} - \frac{\Delta G^\ominus(T_1)}{T_1} = \Delta H^\ominus(p)\left(\frac{1}{T_2} - \frac{1}{T_1}\right)

This equation quickly enables the calculation of the Gibbs free energy change for a chemical reaction at any temperature T2 with knowledge of just the Standard Gibbs free energy change of formation and the Standard enthalpy change of formation for the individual components.

Also, using the reaction isotherm equation,[3] that is

\frac{\Delta G^\ominus}{T} = -R \ln K

which relates the Gibbs energy to a chemical equilibrium constant, the van 't Hoff equation can be derived.[4]

Derivation

Background

The definition of the Gibbs function is

H= G + ST \,\!

where H is the enthalpy defined by:

H= U + pV \,\!

Taking differentials of each definition to find dH and dG, then using the fundamental thermodynamic relation, aka "master equation" (always true for reversible or irreversible processes):

dU= TdS - pdV \,\!

where S is the entropy, V is volume, (minus sign due to reversibility, in which dU = 0: work other than pressure-volume may be done and is equal to −pV) leads to the "reversed" form of the initial fundamental relation into a new master equation:

dG= - SdT + Vdp \,\!

This is the Gibbs free energy for a closed system. The Gibbs–Helmholtz equation can be derived by this second master equation, and the chain rule for partial derivatives.[5]

Sources

  1. ↑ Physical chemistry, P.W. Atkins, Oxford University Press, 1978, ISBN 0-19-855148-7
  2. ↑ Chemical Thermodynamics, D.J.G. Ives, University Chemistry, Macdonald Technical and Scientific, 1971, ISBN 0-356-03736-3
  3. ↑ Chemistry, Matter, and the Universe, R.E. Dickerson, I. Geis, W.A. Benjamin Inc. (USA), 1976, ISBN 0-19-855148-7
  4. ↑ Chemical Thermodynamics, D.J.G. Ives, University Chemistry, Macdonald Technical and Scientific, 1971, ISBN 0-356-03736-3
  5. ↑ physical chemistry, p.W. Atkins, Oxford University press, 1978, ISBN 0-19-855148-7

External links