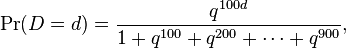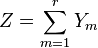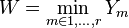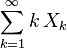Geometric distribution
Probability mass function | ||
Cumulative distribution function | ||
| Parameters | 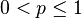 success probability (real) success probability (real) |
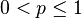 success probability (real) success probability (real) |
|---|---|---|
| Support | k trials where 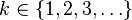 |
k failures where 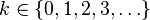 |
| Probability mass function (pmf) | 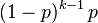 |
 |
| Cumulative distribution function (CDF) |  |
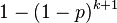 |
| Mean | 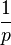 |
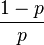 |
| Median | 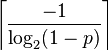 (not unique if |
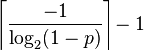 (not unique if |
| Mode | 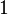 |
 |
| Variance | 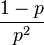 |
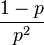 |
| Skewness |  |
 |
| Excess kurtosis | 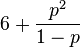 |
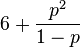 |
| Entropy | 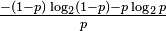 |
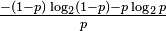 |
| Moment-generating function (mgf) | 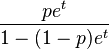 , , for  |
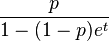 |
| Characteristic function | 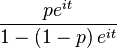 |
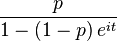 |
In probability theory and statistics, the geometric distribution is either of two discrete probability distributions:
- The probability distribution of the number X of Bernoulli trials needed to get one success, supported on the set { 1, 2, 3, ...}
- The probability distribution of the number Y = X − 1 of failures before the first success, supported on the set { 0, 1, 2, 3, ... }
Which of these one calls "the" geometric distribution is a matter of convention and convenience.
These two different geometric distributions should not be confused with each other. Often, the name shifted geometric distribution is adopted for the former one (distribution of the number X); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the support explicitly.
It’s the probability that the first occurrence of success requires k number of independent trials, each with success probability p. If the probability of success on each trial is p, then the probability that the kth trial (out of k trials) is the first success is
for k = 1, 2, 3, ....
The above form of geometric distribution is used for modeling the number of trials until the first success. By contrast, the following form of geometric distribution is used for modeling number of failures until the first success:
for k = 0, 1, 2, 3, ....
In either case, the sequence of probabilities is a geometric sequence.
For example, suppose an ordinary die is thrown repeatedly until the first time a "1" appears. The probability distribution of the number of times it is thrown is supported on the infinite set { 1, 2, 3, ... } and is a geometric distribution with p = 1/6.
Moments and cumulants
The expected value of a geometrically distributed random variable X is 1/p and the variance is (1 − p)/p2:
Similarly, the expected value of the geometrically distributed random variable Y = X − 1 (where Y corresponds to the pmf listed in the right column) is q/p = (1 − p)/p, and its variance is (1 − p)/p2:
Let μ = (1 − p)/p be the expected value of Y. Then the cumulants 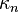 of the probability distribution of Y satisfy the recursion
of the probability distribution of Y satisfy the recursion
Outline of proof: That the expected value is (1 − p)/p can be shown in the following way. Let Y be as above. Then
(The interchange of summation and differentiation is justified by the fact that convergent power series converge uniformly on compact subsets of the set of points where they converge.)
Parameter estimation
For both variants of the geometric distribution, the parameter p can be estimated by equating the expected value with the sample mean. This is the method of moments, which in this case happens to yield maximum likelihood estimates of p.
Specifically, for the first variant let k = k1, ..., kn be a sample where ki ≥ 1 for i = 1, ..., n. Then p can be estimated as
In Bayesian inference, the Beta distribution is the conjugate prior distribution for the parameter p. If this parameter is given a Beta(α, β) prior, then the posterior distribution is
The posterior mean E[p] approaches the maximum likelihood estimate 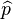 as α and β approach zero.
as α and β approach zero.
In the alternative case, let k1, ..., kn be a sample where ki ≥ 0 for i = 1, ..., n. Then p can be estimated as
The posterior distribution of p given a Beta(α, β) prior is
Again the posterior mean E[p] approaches the maximum likelihood estimate 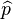 as α and β approach zero.
as α and β approach zero.
Other properties
- The probability-generating functions of X and Y are, respectively,
- Like its continuous analogue (the exponential distribution), the geometric distribution is memoryless. That means that if you intend to repeat an experiment until the first success, then, given that the first success has not yet occurred, the conditional probability distribution of the number of additional trials does not depend on how many failures have been observed. The die one throws or the coin one tosses does not have a "memory" of these failures. The geometric distribution is the only memoryless discrete distribution.
- Among all discrete probability distributions supported on {1, 2, 3, ... } with given expected value μ, the geometric distribution X with parameter p = 1/μ is the one with the largest entropy.
- The geometric distribution of the number Y of failures before the first success is infinitely divisible, i.e., for any positive integer n, there exist independent identically distributed random variables Y1, ..., Yn whose sum has the same distribution that Y has. These will not be geometrically distributed unless n = 1; they follow a negative binomial distribution.
- The decimal digits of the geometrically distributed random variable Y are a sequence of independent (and not identically distributed) random variables. For example, the hundreds digit D has this probability distribution:
- where q = 1 − p, and similarly for the other digits, and, more generally, similarly for numeral systems with other bases than 10. When the base is 2, this shows that a geometrically distributed random variable can be written as a sum of independent random variables whose probability distributions are indecomposable.
- Golomb coding is the optimal prefix code for the geometric discrete distribution.
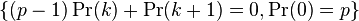
Related distributions
- The geometric distribution Y is a special case of the negative binomial distribution, with r = 1. More generally, if Y1, ..., Yr are independent geometrically distributed variables with parameter p, then the sum
- follows a negative binomial distribution with parameters r and p.[1]
- The geometric distribution is a special case of discrete Compound Poisson distribution.
- If Y1, ..., Yr are independent geometrically distributed variables (with possibly different success parameters pm), then their minimum
- is also geometrically distributed, with parameter
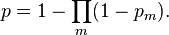
- Suppose 0 < r < 1, and for k = 1, 2, 3, ... the random variable Xk has a Poisson distribution with expected value r k/k. Then
- has a geometric distribution taking values in the set {0, 1, 2, ...}, with expected value r/(1 − r).
- The exponential distribution is the continuous analogue of the geometric distribution. If X is an exponentially distributed random variable with parameter λ, then
- where
 is the floor (or greatest integer) function, is a geometrically distributed random variable with parameter p = 1 − e−λ (thus λ = −ln(1 − p)[2]) and taking values in the set {0, 1, 2, ...}. This can be used to generate geometrically distributed pseudorandom numbers by first generating exponentially distributed pseudorandom numbers from a uniform pseudorandom number generator: then
is the floor (or greatest integer) function, is a geometrically distributed random variable with parameter p = 1 − e−λ (thus λ = −ln(1 − p)[2]) and taking values in the set {0, 1, 2, ...}. This can be used to generate geometrically distributed pseudorandom numbers by first generating exponentially distributed pseudorandom numbers from a uniform pseudorandom number generator: then 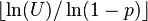 is geometrically distributed with parameter
is geometrically distributed with parameter  , if
, if  is uniformly distributed in [0,1].
is uniformly distributed in [0,1].
- If
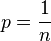 and
and 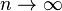 then we get an asymptotic exponential distribution with paramter of
then we get an asymptotic exponential distribution with paramter of 
Since: ![P\left( X>a \right)={{\left( 1-p \right)}^{a}}={{\left( 1-\frac{1}{n} \right)}^{n\frac{1}{n}\left( a \right)}}={{\left[ {{\left( 1-\frac{1}{n} \right)}^{n}} \right]}^{\frac{1}{n}\left( a \right)}}\xrightarrow[n\to \infty ]{}{{\left[ {{e}^{-1}} \right]}^{\frac{1}{n}\left( a \right)}}= {{e}^{-\frac{1}{n}a}}](../I/m/046f0dc46edd19495694f9060e056afd.png)
See also
- Hypergeometric distribution
- Coupon collector's problem
- Compound Poisson distribution
- Negative binomial distribution
References
- ↑ Pitman, Jim. Probability (1993 edition). Springer Publishers. pp 372.
- ↑ http://www.wolframalpha.com/input/?i=inverse+p+%3D+1+-+e^-l
External links
- Geometric distribution at PlanetMath.org.
- Geometric distribution on MathWorld.
- Online geometric distribution calculator
- Online calculator of Geometric distribution
| ||||||||||||||
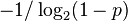 is an integer)
is an integer)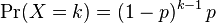
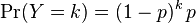
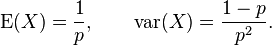
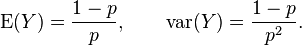
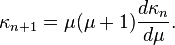
![\begin{align}
\mathrm{E}(Y) & {} =\sum_{k=0}^\infty (1-p)^k p\cdot k \\
& {} =p\sum_{k=0}^\infty(1-p)^k k \\
& {} = p (1-p) \left[\frac{d}{dp}\left(-\sum_{k=0}^\infty (1-p)^k\right)\right] \\
& {} =-p(1-p)\frac{d}{dp}\frac{1}{p}=\frac{1-p}{p}.
\end{align}](../I/m/5b8bce572221c80cf50650505637e659.png)
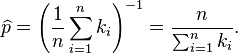



![\begin{align}
G_X(s) & = \frac{s\,p}{1-s\,(1-p)}, \\[10pt]
G_Y(s) & = \frac{p}{1-s\,(1-p)}, \quad |s| < (1-p)^{-1}.
\end{align}](../I/m/0a30cdb42d33013bc92b9001000482e8.png)