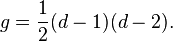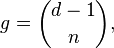Genus–degree formula

In classical algebraic geometry, the genus–degree formula relates the degree d of a non-singular plane curve 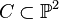$C\subset\mathbb{P}^2$ with its arithmetic genus g via the formula:

g=\frac12 (d-1)(d-2) . \,

If the curve is non-singular the geometric genus and the arithmetic genus are equal, but if the curve is singular, with only ordinary singularities, the geometric genus is smaller. More precisely, an ordinary singularity of multiplicity r decreases the genus by 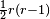$\scriptstyle \frac12 r(r-1)$ .^[1]

Proof

The proof follows immediately from the adjunction formula. For a classical proof see the book of Arbarello, Cornalba, Griffiths and Harris.

Generalization

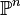For a non-singular hypersurface $H$ of degree d in $\mathbb{P}^n$ of arithmetic genus g the formula becomes:

g=\binom{d-1}{n} , \,

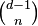where $\tbinom{d-1}{n}$ is the binomial coefficient.

Notes

↑ Semple and Roth, Introduction to Algebraic Geometry, Oxford University Press (repr.1985) ISBN 0-19-853363-2. Pp. 53–54

References

This article incorporates material from the Citizendium article "Genus degree formula", which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.
Arbarello, Cornalba, Griffiths, Harris. Geometry of algebraic curves. vol 1 Springer, ISBN 0-387-90997-4, appendix A.
Griffiths and Harris, Principles of algebraic geometry, Wiley, ISBN 0-471-05059-8, chapter 2, section 1.
Robin Hartshorne (1977): Algebraic geometry, Springer, ISBN 0-387-90244-9.

Kulikov, Viktor S. (2001), "Genus of a curve", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4

Topics in algebraic curves

Rational curves

Elliptic curves

Analytic theory	Elliptic function Elliptic integral Fundamental pair of periods Modular form

Arithmetic theory	Counting points on elliptic curves Division polynomials Hasse's theorem on elliptic curves Mazur's torsion theorem Modular elliptic curve Modularity theorem Mordell–Weil theorem Nagell–Lutz theorem Supersingular elliptic curve Schoof's algorithm Schoof–Elkies–Atkin algorithm

Applications	Elliptic curve cryptography Elliptic curve primality

Higher genus

Plane curves

Riemann surfaces

Constructions

Structure of curves

Divisors on curves	Abel–Jacobi map Brill–Noether theory Clifford's theorem on special divisors Gonality of an algebraic curve Jacobian variety Riemann–Roch theorem Weierstrass point Weil reciprocity law

Moduli	ELSV formula Gromov–Witten invariant Hodge bundle Moduli of algebraic curves Stable curve

Morphisms	Hasse–Witt matrix Riemann–Hurwitz formula Prym variety Weber's theorem

Singularities	Acnode Crunode Cusp Delta invariant Tacnode

Vector bundles	Birkhoff–Grothendieck theorem Stable vector bundle Vector bundles on algebraic curves