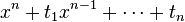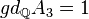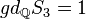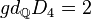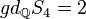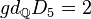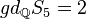Generic polynomial
In Galois theory, a branch of modern algebra, a generic polynomial for a finite group G and field F is a monic polynomial P with coefficients in the field L = F(t1, ..., tn) of F with n indeterminates adjoined, such that the splitting field M of P has Galois group G over L, and such that every extension K/F with Galois group G can be obtained as the splitting field of a polynomial which is the specialization of P resulting from setting the n indeterminates to n elements of F. This is sometimes called F-generic relative to the field F, with a Q-generic polynomial, generic relative to the rational numbers, being called simply generic.
The existence, and especially the construction, of a generic polynomial for a given Galois group provides a complete solution to the inverse Galois problem for that group. However, not all Galois groups have generic polynomials, a counterexample being the cyclic group of order eight.
Groups with generic polynomials
- The symmetric group Sn. This is trivial, as
is a generic polynomial for Sn.
- Cyclic groups Cn, where n is not divisible by eight. Lenstra showed that a cyclic group does not have a generic polynomial if n is divisible by eight, and Smith explicitly constructs such a polynomial in case n is not divisible by eight.
- The cyclic group construction leads to other classes of generic polynomials; in particular the dihedral group Dn has a generic polynomial if and only if n is not divisible by eight.
- The quaternion group Q8.
- Heisenberg groups
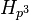 for any odd prime p.
for any odd prime p.
- The alternating group A4.
- The alternating group A5.
- Reflection groups defined over Q, including in particular groups of the root systems for E6, E7, and E8.
- Any group which is a direct product of two groups both of which have generic polynomials.
- Any group which is a wreath product of two groups both of which have generic polynomials.
Examples of generic polynomials
| Group | Generic Polynomial |
|---|---|
| C2 | 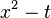 |
| C3 | 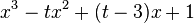 |
| S3 | 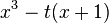 |
| V | 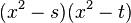 |
| C4 | 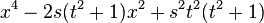 |
| D4 | 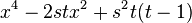 |
| S4 | 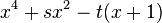 |
| D5 | 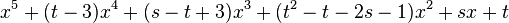 |
| S5 | 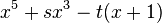 |
Generic polynomials are known for all transitive groups of degree 5 or less.
Generic Dimension
The generic dimension for a finite group G over a field F, denoted 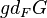 , is defined as the minimal number of parameters in a generic polynomial for G over F, or
, is defined as the minimal number of parameters in a generic polynomial for G over F, or 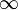 if no generic polynomial exists.
if no generic polynomial exists.
Examples:
Publications
- Jensen, Christian U., Ledet, Arne, and Yui, Noriko, Generic Polynomials, Cambridge University Press, 2002