Generator (category theory)

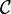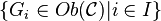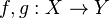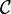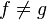In category theory in mathematics a family of generators (or family of separators) of a category $\mathcal C$ is a collection $\{G_i\in Ob(\mathcal C)|i\in I\}$ of objects, indexed by some set I, such that for any two morphisms $f, g: X \rightarrow Y$ in $\mathcal C$ , if $f\neq g$ then there is some i∈I and morphism 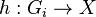$h : G_i \rightarrow X$ , such that the compositions 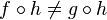$f \circ h \neq g \circ h$ . If the family consists of a single object G, we say it is a generator.

Generators are central to the definition of Grothendieck categories.

The dual concept is called a cogenerator or coseparator.

Examples

In the category of abelian groups, the group of integers 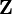$\mathbf Z$ is a generator: If f and g are different, then there is an element 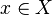$x \in X$ , such that 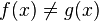$f(x) \neq g(x)$ . Hence the map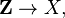 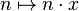$\mathbf Z \rightarrow X,$ $n \mapsto n \cdot x$ suffices.
Similarly, the one-point set is a generator for the category of sets. In fact, any nonempty set is a generator.
In the category of sets, any set with at least two objects is a cogenerator.

References

Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2 , p. 123, section V.7

External links

generator in nLab