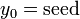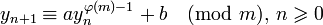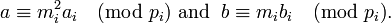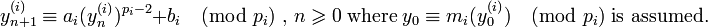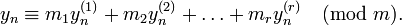Generalized inversive congruential pseudorandom numbers
An approach to nonlinear congruential methods of generating uniform pseudorandom numbers in the interval [0,1) is the Inversive congruential generator with prime modulus. A generalization for arbitrary composite moduli 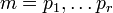 with arbitrary distinct primes
with arbitrary distinct primes 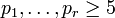 will be present here.
will be present here.
Let 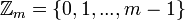 .For integers
.For integers 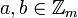 with gcd (a,m) = 1 a generalized inversive congruential sequence
with gcd (a,m) = 1 a generalized inversive congruential sequence 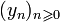 of elements of
of elements of 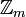 is defined by
is defined by
where 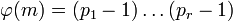 denotes the number of positive integers less than m which are relatively prime to m.
denotes the number of positive integers less than m which are relatively prime to m.
Example
Let take m = 15 = 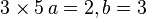 and
and 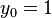 . Hence
. Hence 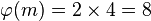 and the sequence
and the sequence 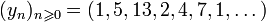 is not maximum.
is not maximum.
The result below shows that these sequences are closely related to the following inversive congruential sequence with prime moduli.
For 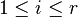 let
let 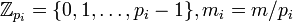 and
and 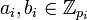 be integers with
be integers with
Let 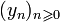 be a sequence of elements of
be a sequence of elements of 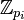 , given by
, given by
Theorem 1
Let 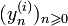 for
for 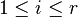 be defined as above.
Then
be defined as above.
Then
This theorem shows that an implementation of Generalized Inversive Congruential Generator is possible,where exact integer computations have to be performed only in 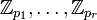 but not in
but not in 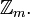
Proof:
First, observe that 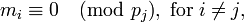 and hence
and hence 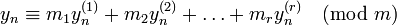 if and only if
if and only if 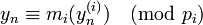 , for
, for 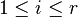 which will be shown on induction on
which will be shown on induction on 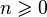 .
.
Recall that 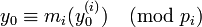 is assumed for
is assumed for 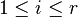 . Now, suppose that
. Now, suppose that 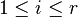 and
and 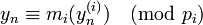 for some integer
for some integer 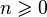 . Then straightforward calculations and Fermat's Theorem yield
. Then straightforward calculations and Fermat's Theorem yield
-
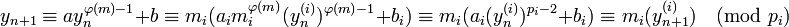 ,
,
which implies the desired result.
Generalized Inversive Congruential Pseudorandom Numbers are well equidistributed in one dimension. A reliable theoretical approach for assessing their statistical independence properties is based on the discrepancy of s-tuples of pseudorandom numbers.
Discrepancy bounds of the GIC Generator
We use the notation 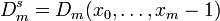 where
where 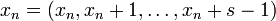 ∈
∈ 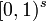 of Generalized Inversive Congruential Pseudorandom Numbers for
of Generalized Inversive Congruential Pseudorandom Numbers for 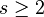 .
.
Higher bound
- Let
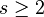
- Then the discrepancy
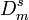 satisfies
satisfies 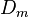
 <
< 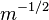 ×
× 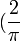 ×
× 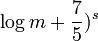 ×
× 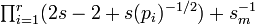 for any Generalized Inversive Congruential operator.
for any Generalized Inversive Congruential operator.
Lower bound:
- There exist Generalized Inversive Congruential Generators with
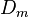
 ≥
≥ 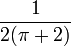 ×
× 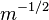 : ×
: × 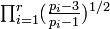 for all dimension s :≥ 2.
for all dimension s :≥ 2.
For a fixed number r of prime factors of m, Theorem 2 shows that 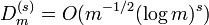 for any Generalized Inversive Congruential Sequence. In this case Theorem 3 implies that there exist Generalized Inversive Congruential Generators having a discrepancy
for any Generalized Inversive Congruential Sequence. In this case Theorem 3 implies that there exist Generalized Inversive Congruential Generators having a discrepancy 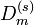 which is at least of the order of magnitude
which is at least of the order of magnitude 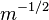 for all dimension
for all dimension 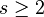 . However,if m is composed only of small primes, then r can be of an order of magnitude
. However,if m is composed only of small primes, then r can be of an order of magnitude 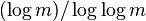 and hence
and hence 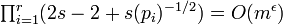 for every
for every 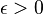 .[1] Therefore, one obtains in the general case
.[1] Therefore, one obtains in the general case 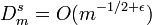 for every
for every 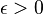 .
.
Since 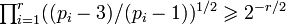 , similar arguments imply that in the general case the lower bound in Theorem 3 is at least of the order of magnitude
, similar arguments imply that in the general case the lower bound in Theorem 3 is at least of the order of magnitude
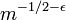 for every
for every 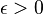 . It is this range of magnitudes where one also finds the discrepancy of m independent and uniformly distributed random points which almost always has the order of magnitude
. It is this range of magnitudes where one also finds the discrepancy of m independent and uniformly distributed random points which almost always has the order of magnitude
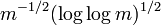 according to the law of the iterated logarithm for discrepancies.[2] In this sense, Generalized Inversive Congruential Pseudo-random Numbers model true random numbers very closely.
according to the law of the iterated logarithm for discrepancies.[2] In this sense, Generalized Inversive Congruential Pseudo-random Numbers model true random numbers very closely.
See also
- Pseudorandom number generator
- List of random number generators
- Linear congruential generator
- Inversive congruential generator
- Naor-Reingold Pseudorandom Function