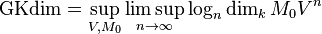Gelfand–Kirillov dimension

In algebra, the Gelfand–Kirillov dimension (or GK dimension) of a right module M over a k-algebra A is:

\operatorname{GKdim} = \sup_{V, M_0} \limsup_{n \to \infty} \log_n \dim_k M_0 V^n

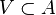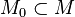where the sup is taken over all finite-dimensional subspaces $V \subset A$ and $M_0 \subset M$ .

An algebra is said to have polynomial growth if its Gelfand–Kirillov dimension is finite.

Basic facts

The Gelfand–Kirillov dimension of a finitely generated commutative algebra A over a field is the Krull dimension of A (or equivalently the transcendence degree of the field of fractions of A over the base field.)
In particular, the GK dimension of the polynomial ring $k[x_1, \dots, x_n]$ Is n.
(Warfield) For any real number r ≥ 2, there exists a finitely generated algebra whose GK dimension is r.^[1]

In the theory of D-Modules

Given a right module M over the Weyl algebra 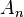$A_n$ , the Gelfand–Kirillov dimension of M over the Weyl algebra coincides with the dimension of M, which is by definition the degree of the Hilbert polynomial of M. This enables to prove additivity in short exact sequences for the Gelfand–Kirillov dimension and finally to prove Bernstein's inequality, which states that the dimension of M must be at least n. This leads to the definition of holonomic D-Modules as those with the minimal dimension n, and these modules play a great role in the geometric Langlands program.

References

↑ Artin 1999, Theorem VI.2.1.

Smith, S. Paul; Zhang, James J. (1998). "A remark on Gelfand–Kirillov dimension". Proceedings of the American Mathematical Society 126 (2): 349–352.
Coutinho: A primer of algebraic D-modules. Cambridge, 1995

Gelfand–Kirillov dimension

Basic facts

In the theory of D-Modules

References

Further reading