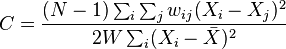Geary's C
Geary's C is a measure of spatial autocorrelation or an attempt to determine if adjacent observations of the same phenomenon are correlated. Spatial autocorrelation is more complex than autocorrelation because the correlation is multi-dimensional and bi-directional.
Geary's C is defined as
where 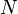 is the number of spatial units indexed by
is the number of spatial units indexed by 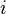 and
and 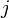 ;
;  is the variable of interest;
is the variable of interest; 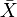 is the mean of
is the mean of  ;
; 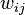 is a matrix of spatial weights; and
is a matrix of spatial weights; and 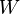 is the sum of all
is the sum of all 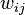 .
.
The value of Geary's C lies between 0 and 2. 1 means no spatial autocorrelation. Values lower than 1 demonstrate increasing positive spatial autocorrelation, whilst values higher than 1 illustrate increasing negative spatial autocorrelation.
Geary's C is inversely related to Moran's I, but it is not identical. Moran's I is a measure of global spatial autocorrelation, while Geary's C is more sensitive to local spatial autocorrelation.
Geary's C is also known as Geary's contiguity ratio or simply Geary's ratio.[1]
This statistic was developed by Roy C. Geary.[2]
Sources
- ↑ J. N. R. Jeffers (1973). "A Basic Subroutine for Geary's Contiguity Ratio". Journal of the Royal Statistical Society (Series D) (Wiley) 22 (4).
- ↑ Geary, R. C. (1954). "The Contiguity Ratio and Statistical Mapping". The Incorporated Statistician (The Incorporated Statistician) 5 (3): 115–145. doi:10.2307/2986645. JSTOR 2986645.