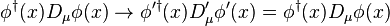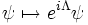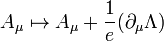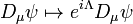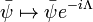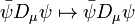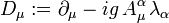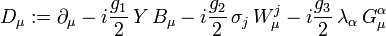Gauge covariant derivative
The gauge covariant derivative is a generalization of the covariant derivative used in general relativity. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations. Likewise, the gauge covariant derivative is the ordinary derivative modified in such a way as to make it behave like a true vector operator, so that equations written using the covariant derivative preserve their physical properties under gauge transformations.
Fluid dynamics
In fluid dynamics, the gauge covariant derivative of a fluid may be defined as
where 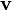 is a velocity vector field of a fluid.
is a velocity vector field of a fluid.
Gauge theory
In gauge theory, which studies a particular class of fields which are of importance in quantum field theory, the minimally-coupled gauge covariant derivative is defined as
where 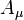 is the electromagnetic vector potential.
is the electromagnetic vector potential.
(Note that this is valid for a Minkowski metric of signature 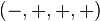 , which is used in this article. For
, which is used in this article. For 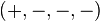 the minus becomes a plus.)
the minus becomes a plus.)
Construction of the covariant derivative throught Gauge covariance requirement
Consider a generic, possibly non abelian, Gauge transformation given by
where 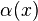 is an element of the Lie algebra associated with the Lie group of transformations, and can be expressed in terms of the generators as
is an element of the Lie algebra associated with the Lie group of transformations, and can be expressed in terms of the generators as 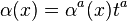 .
.
The partial derivative 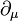 transforms accordingly as
transforms accordingly as
and a kinetic term of the form 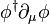 is thus not invariant under this transformation.
is thus not invariant under this transformation.
We can introduce the covariant derivative 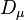 in this context as a generalization of the partial derivative
in this context as a generalization of the partial derivative 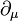 which transforms covariantly under the Gauge transformation, i.e. an object satisfying
which transforms covariantly under the Gauge transformation, i.e. an object satisfying
which in operatorial form takes the form
We thus compute (omitting the explicit  dependences for brevity)
dependences for brevity)
![D_\mu \phi \rightarrow D'_\mu U \phi = UD_\mu \phi + (\delta D_\mu U + [D_\mu,U])\phi](../I/m/6b500a592f183a1f10b93e1ea38cfe55.png) ,
,
where
The requirement for 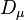 to transform covariantly is now translated in the condition
to transform covariantly is now translated in the condition
To obtain an explicit expression we make the Ansatz
from which it follows that
and
which, using 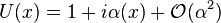 , takes the form
, takes the form
We have thus found an object 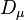 such that
such that
Quantum electrodynamics
If a gauge transformation is given by
and for the gauge potential
then 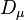 transforms as
transforms as
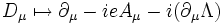 ,
,
and 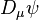 transforms as
transforms as
and 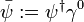 transforms as
transforms as
so that
and 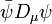 in the QED Lagrangian is therefore gauge invariant, and the gauge covariant derivative is thus named aptly.
in the QED Lagrangian is therefore gauge invariant, and the gauge covariant derivative is thus named aptly.
On the other hand, the non-covariant derivative 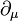 would not preserve the Lagrangian's gauge symmetry, since
would not preserve the Lagrangian's gauge symmetry, since
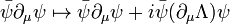 .
.
Quantum chromodynamics
In quantum chromodynamics, the gauge covariant derivative is[1]
where  is the coupling constant,
is the coupling constant,  is the gluon gauge field, for eight different gluons
is the gluon gauge field, for eight different gluons 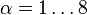 ,
, 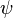 is a four-component Dirac spinor, and where
is a four-component Dirac spinor, and where 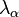 is one of the eight Gell-Mann matrices,
is one of the eight Gell-Mann matrices, 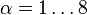 .
.
Standard Model
The covariant derivative in the Standard Model can be expressed in the following form:[2]
See also
- Kinetic momentum
- Connection (mathematics)
- Minimal coupling
- Ricci calculus
References
- ↑ http://www.fuw.edu.pl/~dobaczew/maub-42w/node9.html
- ↑ See e.g. eq. 3.116 in C. Tully, Elementary Particle Physics in a Nutshell, 2011, Princeton University Press.
- Tsutomu Kambe, Gauge Principle For Ideal Fluids And Variational Principle. (PDF file.)
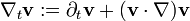
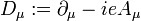
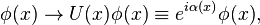
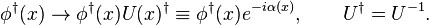
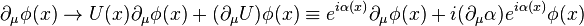
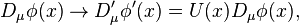
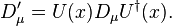
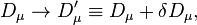
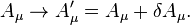
![(\delta D_\mu U + [D_\mu,U])\phi = 0.](../I/m/b0311e1de44c6a8d91a1cc37a995eff3.png)
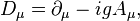
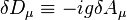
![\delta A_\mu = [U,A_\mu]U^\dagger -\frac{i}{g} (\partial_\mu U)U^\dagger](../I/m/a23b52f7794a753e09e939d7e86edc23.png)
![\delta A_\mu = \frac{1}{g} ( \partial_\mu \alpha - ig [A_\mu,\alpha] ) + \mathcal{O}(\alpha^2) = \frac{1}{g} D_\mu \alpha + \mathcal{O}(\alpha^2)](../I/m/19491e37acfc205621d2a1a4becd01c3.png)