Gamma/Gompertz distribution
|
Probability density function
| |
|
Cumulative distribution function
| |
| Parameters |
 |
|---|---|
| Support |
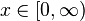 |
 | |
| CDF |
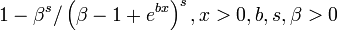 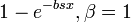 |
| Mean |
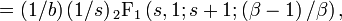 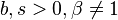 ![=\left(1/b\right)\left[\beta/\left(\beta-1\right)\right]\ln\left(\beta\right),](../I/m/7aa02e026c2b1b68e133319eb632f893.png) 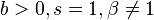 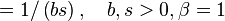 |
| Median |
![\left(1/b\right)\ln\{\beta\left[\left(1/2\right)^{-1/s}-1\right]+1\}](../I/m/67a86be9618ef904ec9e29ef73b62eff.png) |
| Mode |
![\begin{align}x^*& = (1/b)\ln\left[(1/s)(\beta-1)\right], \\&\text{with } 0<\text{F}(x^*)<1-(\beta s)^s/\left[(\beta-1)(s+1)\right]^s<0.632121,\\& \beta > s+1\\& = 0, \quad \beta\le s+1\\\end{align}](../I/m/80672ca9697b9c3126e397de33f3555b.png) |
| Variance |
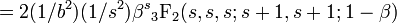 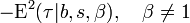 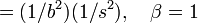  ![{_3\text{F}_2}(a,b,c;d,e;z) = \sum_{k=0}^\infty\{(a)_k(b)_k(c)_k/[(d)_k(e)_k]\}z^k/k!](../I/m/8118b8d2cbefab5b410ddaa9accea4a0.png) 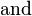 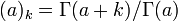 |
| MGF |
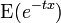 ![=\beta^{s}[sb/(t+sb)]{_2\text{F}_1}(s+1,(t/b)+s;(t/b)+s+1;1-\beta),](../I/m/2a4421438e9d0e432b109807f5d752b2.png) 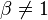 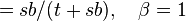 ![\text{with }{_2\text{F}_1}(a,b;c;z) = \sum_{k=0}^\infty[(a)_k(b)_k/(c)_k]z^k/k!](../I/m/f9ad9f4b73dc12e0ac3b2cf7f0fe460c.png) |
In probability and statistics, the Gamma/Gompertz distribution is a continuous probability distribution. It has been used as an aggregate-level model of customer lifetime and a model of mortality risks.
Specification
Probability density function
The probability density function of the Gamma/Gompertz distribution is:
where 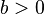 is the scale parameter and
is the scale parameter and 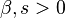 are the shape parameters of the Gamma/Gompertz distribution.
are the shape parameters of the Gamma/Gompertz distribution.
Cumulative distribution function
The cumulative distribution function of the Gamma/Gompertz distribution is:
Moment generating function
The moment generating function is given by:
where ![{_2\text{F}_1}(a,b;c;z) = \sum_{k=0}^\infty[(a)_k(b)_k/(c)_k]z^k/k!](../I/m/6833773d4b5370df2025df650b0660df.png) is a Hypergeometric function.
is a Hypergeometric function.
Properties
The Gamma/Gompertz distribution is a flexible distribution that can be skewed to the right and to the left.
Related distributions
- When β = 1, this reduces to an Exponential distribution with parameter sb.
- The gamma distribution is a natural conjugate prior to a Gompertz likelihood with known, scale parameter
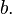 [1]
[1] - When the shape parameter
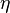 of a Gompertz distribution varies according to a gamma distribution with shape parameter
of a Gompertz distribution varies according to a gamma distribution with shape parameter 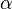 and scale parameter
and scale parameter 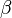 (mean =
(mean = 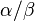 ), the distribution of
), the distribution of 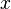 is Gamma/Gompertz.[1]
is Gamma/Gompertz.[1]
See also
Notes
References
- Bemmaor, Albert C.; Glady, Nicolas (2012). "Modeling Purchasing Behavior With Sudden 'Death': A Flexible Customer Lifetime Model". Management Science 58 (5): 1012–1021. doi:10.1287/mnsc.1110.1461.
- Bemmaor, Albert C.; Glady, Nicolas (2011). "Implementing the Gamma/Gompertz/NBD Model in MATLAB". Cergy-Pontoise: ESSEC Business School.
- Gompertz, B. (1825). "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies". Philosophical Transactions of the Royal Society of London 115: 513–583. doi:10.1098/rstl.1825.0026. JSTOR 107756.
- Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1995). "Continuous Univariate Distributions" 2 (2nd ed.). New York: John Wiley & Sons. pp. 25–26. ISBN 0-471-58494-0.
- Manton, K. G.; Stallard, E.; Vaupel, J. W. (1986). "Alternative Models for the Heterogeneity of Mortality Risks Among the Aged". Journal of the American Statistical Association 81: 635–644. doi:10.1080/01621459.1986.10478316.


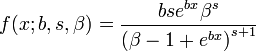
![\begin{align}F(x;b,s,\beta)& = 1 - \frac{\beta^s}{\left(\beta-1+e^{bx}\right)^s}, {\ }x>0, {\ } b,s,\beta>0 \\[6pt]
& = 1-e^{-bsx}, {\ }\beta=1\\\end{align}](../I/m/46c2479748b7310c92ef7285a2200343.png)
