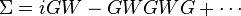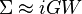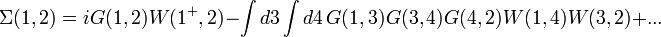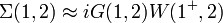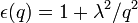GW approximation
The GW approximation (GWA) is an approximation made in order to calculate the self-energy of a many-body system of electrons. The approximation is that the expansion of the self-energy Σ in terms of the single particle Green's function G and the screened Coulomb interaction W (in units of  )
)
can be truncated after the first term:
Another way to say the same thing is that that self-energy is expanded in a formal Taylor series in powers of the screened interaction W and the lowest order term is kept in the expansion in GWA.
The above formulae are schematic in nature and show the overall idea of the approximation. More precisely, if we label an electron coordinate with its position, spin, and time and bundle all three into a composite index (the numbers 1, 2, etc.), we have
where the "+" superscript means the time index is shifted forward by an infinitesimal amount. The GWA is then
To put this in context, if one replaces W by the bare Coulomb interaction (i.e. the usual 1/r interaction), one generates the standard perturbative series for the self-energy found in most many-body textbooks. The GWA with W replaced by the bare Coulomb yields nothing other than the Hartree–Fock exchange potential (self-energy). Therefore, loosely speaking, the GWA represents a type of dynamically screened Hartree–Fock self-energy.
In a solid state system, the series for the self-energy in terms of W should converge much faster than the traditional series in the bare Coulomb interaction. This is because the screening of the medium reduces the effective strength of the Coulomb interaction: for example, if one places an electron at some position in a material and asks what the potential is at some other position in the material, the value is smaller than given by the bare Coulomb interaction (inverse distance between the points) because the other electrons in the medium polarize (move or distort their electronic states) so as to screen the electric field. Therefore, W is a smaller quantity than the bare Coulomb interaction so that a series in W should have higher hopes of converging quickly.
To see the more rapid convergence, we can consider the simplest example involving the homogeneous or uniform electron gas which is characterized by an electron density or equivalently the average electron-electron separation or Wigner-Seitz radius 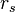 . (We only present a scaling argument and will not compute numerical prefactors that are order unity.) Here are the key steps:
. (We only present a scaling argument and will not compute numerical prefactors that are order unity.) Here are the key steps:
- The kinetic energy of an electron scales as
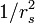
- The average electron-electron repulsion from the bare (unscreened) Coulomb interaction scales as
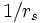 (simply the inverse of the typical separation)
(simply the inverse of the typical separation) - The electron gas dielectric function in the simplest Thomas–Fermi screening model for a wave vector
 is
is
where  is the screening wave number that scales as
is the screening wave number that scales as 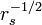
- Typical wave vectors
 scale as
scale as 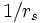 (again typical inverse separation)
(again typical inverse separation) - Hence a typical screening value is
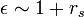
- The screened Coulomb interaction is
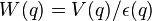
Thus for the bare Coulomb interaction, the ratio of Coulomb to kinetic energy is of order 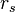 which is of order 2-5 for a typical metal and not small at all: in other words, the bare Coulomb interaction is rather strong and makes for a poor perturbative expansion. On the other hand, the ratio of a typical
which is of order 2-5 for a typical metal and not small at all: in other words, the bare Coulomb interaction is rather strong and makes for a poor perturbative expansion. On the other hand, the ratio of a typical  to the kinetic energy is greatly reduced by the screening and is of order
to the kinetic energy is greatly reduced by the screening and is of order 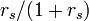 which is well behaved and smaller than unity even for large
which is well behaved and smaller than unity even for large 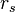 : the screened
interaction is much weaker and is more likely to give a rapidly converging perturbative series.
: the screened
interaction is much weaker and is more likely to give a rapidly converging perturbative series.
Software implementing the GW approximation
- ABINIT - plane-wave pseudopotential method
- BerkeleyGW - plane-wave pseudopotential method
- FHI-aims - Numeric atom-centered orbitals method
- Fiesta - Gaussian pseudopotential method
- Quantum ESPRESSO - Wannier-function pseudopotential method
- SaX - plane-wave pseudopotential method
- Spex - full-potential (linearized) augmented plane-wave (FP-LAPW) method
- VASP - projector-augmented-wave (PAW) method
- YAMBO code - plane-wave pseudopotential method
- FHI-gap - an all-electron GW code based on augmented plane-waves, currently interfaced with WIEN2k
References
- Hedin, Lars (1965). "New Method for Calculating the One-Particle Green's Function with Application to the Electron-Gas Problem". Phys. Rev. 139 (3A): A796–A823. Bibcode:1965PhRv..139..796H. doi:10.1103/PhysRev.139.A796.
- Aulbur, W.G.; Jönsson, L.; Wilkins, J.W. (2000). "Quasiparticle Calculations in Solids". Solid State Physics 54: 1–218. doi:10.1016/S0081-1947(08)60248-9.
- Aryasetiawan, F.; Gunnarsson, O. (1998). "The GW Method". Rep. Prog. Phys. 61 (3): 237. arXiv:cond-mat/9712013. Bibcode:1998RPPh...61..237A. doi:10.1088/0034-4885/61/3/002.
- Aryasetiawan, Ferdi. "Correlation effects in solids from first principles".
- Electron Correlation in the Solid State, Norman H. March (editor), World Scientific Publishing Company
- The key publications concerning the application of the GW approximation
- Picture of Lars Hedin, inventor of GW