GIT quotient

In algebraic geometry, an affine GIT quotient, or affine geometric invariant theory quotient, of an affine scheme 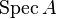with action by a group scheme G is the affine scheme 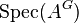, the prime spectrum of the ring of invariants of A, and is denoted by 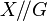. A GIT quotient is a categorical quotient: any invariant morphism uniquely factors through it.

Taking Proj (of a graded ring) instead of 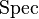, one obtains a projective GIT quotient (which is a quotient of the set of semistable points.)

A GIT quotient is a categorical quotient (of the semistable points); i.e., "the" quotient. Since the categorical quotient is unique, if there is a geometric quotient, then the two notions coincide: for example, one has for an algebraic group G over a field k and closed subgroup H.

If X is a complex smooth projective variety, then the GIT quotient of X by G is homeomorphic to the symplectic quotient of X by a maximal compact subgroup of G (Kempf–Ness theorem).

References

• M. Brion, "Introduction to actions of algebraic groups"
• Doran, Brent; Kirwan, Frances (2007). "Towards non-reductive geometric invariant theory". v1. arXiv:math/0703131. 
• Victoria Hoskins, Quotients in algebraic and symplectic geometry
• F. C. Kirwan, Cohomology of Quotients in Complex and Algebraic Geometry, Mathematical Notes 31, Princeton University Press, Princeton N. J., 1984.
• Mukai, S. (2002). An introduction to invariants and moduli. Cambridge Studies in Advanced Mathematics 81. ISBN 978-0-521-80906-1. 
• Mumford, David; Fogarty, J.; Kirwan, F. (1994). Geometric invariant theory. Ergebnisse der Mathematik und ihrer Grenzgebiete (2) [Results in Mathematics and Related Areas (2)] 34 (3rd ed.). Berlin, New York: Springer-Verlag. ISBN 978-3-540-56963-3. MR 1304906. 
• Thomas, R. P. (2006). "Notes on GIT and symplectic reduction for bundles and varieties". Surveys in Differential Geometry, (): A Tribute to Professor S.-S. Chern. v3 10 (2006). arXiv:math/0512411. 

See also

• quotient stack
• Draft:Chow quotient
• character variety