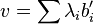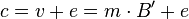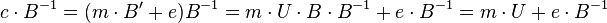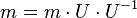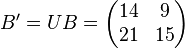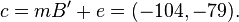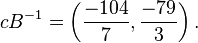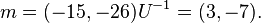GGH encryption scheme
The Goldreich–Goldwasser–Halevi (GGH) lattice-based cryptosystem is an asymmetric cryptosystem based on lattices. There is also a GGH signature scheme.
The Goldreich–Goldwasser–Halevi (GGH) cryptosystem makes use of the fact that the closest vector problem can be a hard problem. It was published in 1997 and uses a trapdoor one-way function that is relying on the difficulty of lattice reduction. The idea included in this trapdoor function is that, given any basis for a lattice, it is easy to generate a vector which is close to a lattice point, for example taking a lattice point and adding a small error vector. But to return from this erroneous vector to the original lattice point a special basis is needed.
The GGH encryption scheme was cryptanalyzed in 1999 by Phong Q. Nguyen.
Operation
GGH involves a private key and a public key.
The private key is a basis  of a lattice
of a lattice  with good properties (such as short nearly orthogonal vectors) and a unimodular matrix
with good properties (such as short nearly orthogonal vectors) and a unimodular matrix  .
.
The public key is another basis of the lattice  of the form
of the form 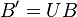 .
.
For some chosen M, the message space consists of the vector 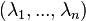 in the range
in the range 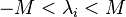 .
.
Encryption
Given a message 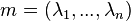 , error
, error  , and a
public key
, and a
public key 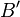 compute
compute
In matrix notation this is
-
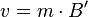 .
.
Remember  consists of integer values, and
consists of integer values, and 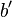 is a lattice point, so v is also a lattice point. The ciphertext is then
is a lattice point, so v is also a lattice point. The ciphertext is then
Decryption
To decrypt the cyphertext one computes
The Babai rounding technique will be used to remove the term 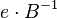 as long as it is small enough. Finally compute
as long as it is small enough. Finally compute
to get the messagetext.
Example
Let 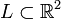 be a lattice with the basis
be a lattice with the basis  and its inverse
and its inverse 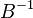
-
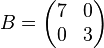 and
and 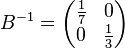
With
-
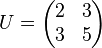 and
and -
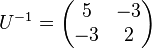
this gives
Let the message be 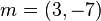 and the error vector
and the error vector 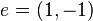 . Then the ciphertext is
. Then the ciphertext is
To decrypt one must compute
This is rounded to 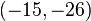 and the message is recovered with
and the message is recovered with
Security of the scheme
1999 Nguyen showed at the Crypto conference that the GGH encryption scheme has a flaw in the design of the schemes. He showed that every ciphertext reveals information about the plaintext and that the problem of decryption could be turned into a special closest vector problem much easier to solve than the general CVP.
Bibliography
- Oded Goldreich, Shafi Goldwasser, and Shai Halevi. Public-key cryptosystems from lattice reduction problems. In CRYPTO ’97: Proceedings of the 17th Annual International Cryptology Conference on Advances in Cryptology, pages 112–131, London, UK, 1997. Springer-Verlag.
- Phong Q. Nguyen. Cryptanalysis of the Goldreich–Goldwasser–Halevi Cryptosystem from Crypto ’97. In CRYPTO ’99: Proceedings of the 19th Annual International Cryptology Conference on Advances in Cryptology, pages 288–304, London, UK, 1999. Springer-Verlag.